Adding and Subtracting Fractions

Adding and subtracting fractions with unlike denominators typically isn’t introduced until fifth grade, so this concept isn’t too difficult for fourth graders. The most common mistake is for students to add or subtract the denominator, because they aren’t thinking about the meaning of the fraction. Fractions greater than one can also cause a challenge when adding and subtracting fractions. To prevent this, I have students work with Cuisenaire rods at the beginning of this series of lessons. You can find the lessons below here.

Conceptual Addition

In this activity, students use Cuisenaire Rods to understand addition as joining of parts of the same size whole. This is a great way to allow students to see why the denominator doesn’t change when you add fractions.

This lesson helps students to see that the number of parts in a whole doesn’t change when you combine fractional parts-only the counting number (numerator) changes. It’s also important that students have experience with mixed numbers and improper fractions within instruction. This prevents students from over generalizing.

This lesson can also be completed digitally. I have students copy and paste their models into the slide. You can use Braining Camp, Math Playground, or PBS Learning Media for the manipulatives.

Problem Solving With Addition Games

This lesson gives students a problem-solving experience that also provides practice with combining fractions multiple ways. You’ll need dice with unit fractions. I covered my existing dice with stickers that I wrote on.

The object of the game is to earn as many points as possible by combining unit fractions to equal one whole. Each round is worth a potential of ten points. But, it’s tricky to get all ten points. Students may only be able to combine two, three, or four fractions, but the goal is to get as high a score as possible.

For example, in the first row, the student would have scored 6 points by adding 1/2 + 1/4 + 1/4.  In the second row the student would earn 10 points by adding 1/6+1/6+1/6+1/6+1/3. If students are ready to add fractions with unlike denominators, I let them, but it’s certainly not necessary for the lesson.

In a different activity, students use their knowledge of equivalent fractions to decompose and decompose addends to reach a whole. During this lesson, encourage students to use the commutative and associative properties to allow them to get to the next whole number more easily. This gives students important practice composing and decomposing fractions.

Subtract Fractions

Once students have experience adding fractions, it’s time to introduce subtracting fractions. Once again, I use Cuisenaire Rods to introduce this concept. This is typically easy for students, because the same patterns apply to subtraction. However, most students run into a road block when they encounter a problem that requires regrouping.

I often model one of the basic problems with students to make sure they understand the directions. Then, I have them try a problem that will require regrouping on their own. I don’t tell them that they will need to regroup or explain what to do. Instead, I let them problem solve for a few minutes to see if they can discover what to do own their own. I’ve discovered that students with moderate fraction sense will be able to construct this own their own. This lets me focus on the students who need additional instruction in a small group.

This lesson can also be completed digitally. Students can copy and paste their digital work onto the included Google Slide to show their work. At this point, these representations are incredibly important for students.

Regrouping when subtracting fractions is not easy. After giving students time to explore through hands-on learning, I’ve found that pictorial representations using pattern blocks are incredibly helpful. Students first partition and shade in the quantity they begin with. For example, in the first problem, students shade three and one-sixth. Then, they show how to regroup to take away one and four-sixths.

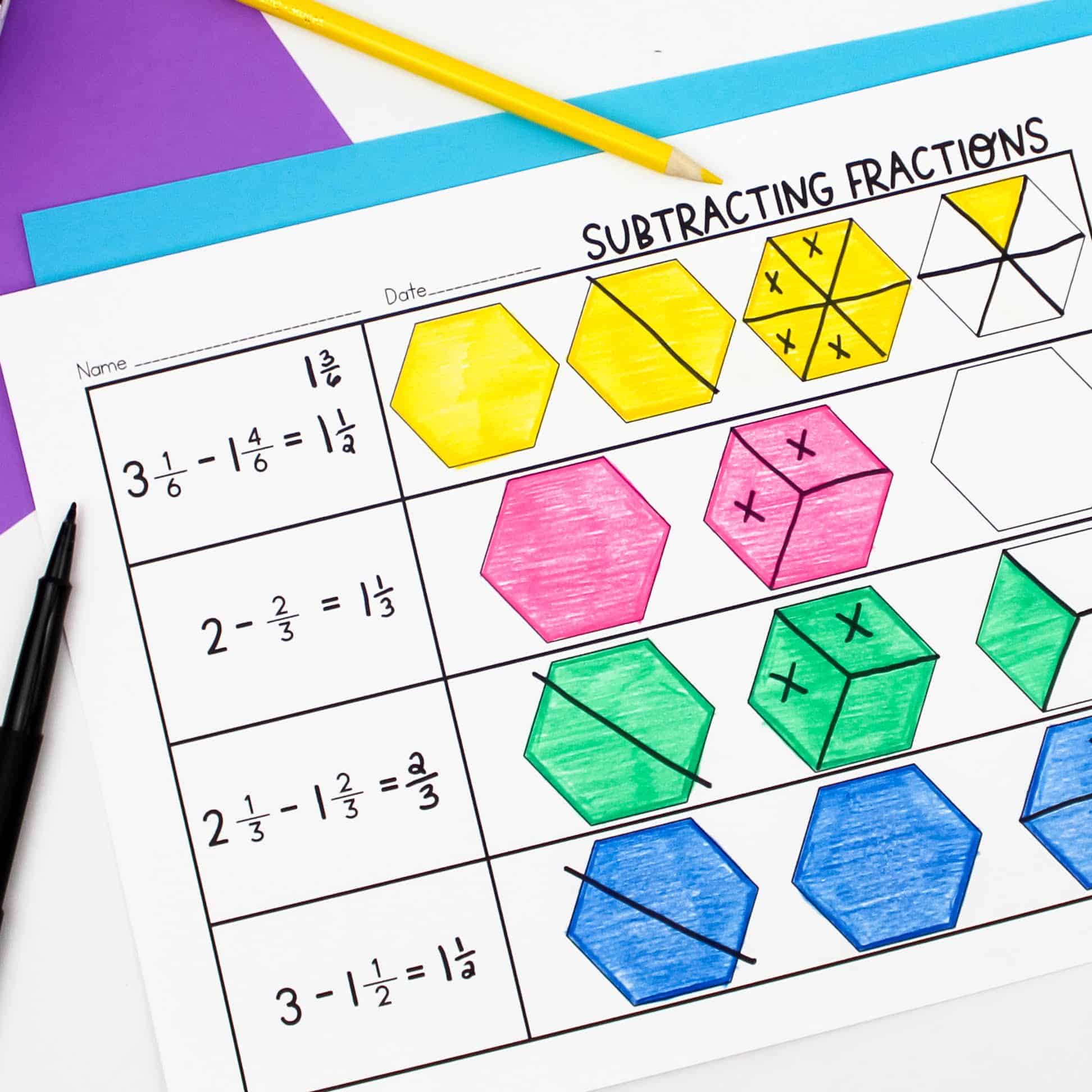
As students progress, they can draw the models using grid paper. In this example, students drew two and one-third. Then, they modeled how to use regrouping to remove one and two-thirds.

Within your adding and subtracting fractions instruction, it’s important to continuously embed authentic word problems. It can be tempting to save that for last, but students gain a much deeper understanding when concepts are taught through word problems. I try to include a variety of problem types, especially sharing problems.

Students should complete a variety of problem solving tasks, including nontraditional problems for adding and subtracting fractions. This is where you get to dig-in and have students apply what concepts they’ve learned. In this type of problem, students cannot solely rely on memorization and procedures but have to use their understanding of fractions to solve real-world problems.

I love any opportunity to integrate math and art. In this task, students design three quilts using four different colors on 24 total squares (for each quilt). Then, students add and subtract fractions based on their designs. When completing this lesson, I do set some parameters. Students quickly realize they can use six of each color, which makes the comparison portion a little too easy!

This adding and subtracting fractions pizza activity is always a student favorite. Students design pizzas based on the guest check for various pizza orders. Then, they use the pizzas to solve problems about the pizza. You can have a lot of fun with this lesson. I’ve seen some teachers go all out with pizza boxes and everything!

You can find all of these adding and subtracting fraction lessons here. If you want to find more information and resources for teaching fractions, don’t miss this post.