
After I finish my place value remediation lessons, I begin my lessons for subtraction and addition remediation. I always begin with addition, but I do intermix fact families as I teach addition. This allows subtraction to become a more natural form of computation for students. These lessons begin very easy, but they build a conceptual understanding of addition and subtraction that will later help students problem solve and solve word problems with larger numbers. During this time, I do not focus on the memorization of addition and subtraction facts, because I don’t want to focus too much time on memorization and forfeit understanding.

I begin by reviewing 10 frames with students. I make sure students realize that the dots plus the spaces equal 10. Students use 2-sided counters to practice all the combinations that make 10. I try to have students practice all combinations of every basic fact. For example the basic fact 3 + 7 = 10 is linked to all these problems: 3+7=10, ?+3=10, 10-?=3, ?+7=10, 7+?=10, 10-3=?, 3+?=10, 10-7=? ?-3=7, 7+3=?, ?-7=3, 10-?=7. This allows students to begin seeing the relationship between addition and subtraction.

In the second activity, I give students a collection of little 10-frames. Each student has a set of 10 tens and a set of frames for each number 1-5 with an extra 5. Students use the 10-frames to develop the idea of one more than or one less than with multiples of ten. For example if 6 is one less than 7, then 60 is one less than 70. Then, I have students think about larger numbers in parts and have students think of ways to take apart multiples of ten. In another activity, I challenge students to build numbers in as many different ways as possible allowing students to develop a better understanding of parts and wholes. For example, how many ways can students build 76? The most obvious way is 70+6, but have students determine different ways to build the number.

I do another task where students solve addition problems using representations for different numbers. This forces students to think about what they are doing, rather than relying on steps and procedures. In this lesson, students are given a number and a model of base-ten pieces. Students should should add the base-ten pieces to the given number and should be able to solve the addition problem mentally. In a different activity that doesn’t require any materials, I say a number between 50 and 100. I have students respond with 50 and ____. For example, with the number 75, students would say 50 and 25. This allows students to begin reasoning with and applying nice numbers to their computation strategies. This will play a significant role in future number talks.

I LOVE this compatible pairs activity! In this lesson, I have students look at the task cards to try and find compatible pairs. There are four different task cards, each with a different level of difficult. In card one, students look for ways to make 50. In card two, students look for ways to make 100. In card three, students look for ways to make 500. In card four, students look for ways to make 1,000. As students progress through the cards, they start to apply some pretty advanced addition strategies.
In a different activity, I provide pairs of students with a set of little ten-frame cards for each of two students. One student should make a number and one student should make a number. Both numbers should be placed where students can easily see the cards. The two numbers should be added together. Students may check their work with the ten frames.

Another activity to help students understand addition and subtraction is to have students complete the fragmented hundreds charts. Students should think about one more and one less, as well as ten greater and ten less. If you laminate the cards, they may write on them with a dry erase marker. Otherwise, print one copy for each student in the group.
A more challenging activity is to give students a cup with place value chips. I typically include ones, tens, and hundreds chips, but you can add thousands or remove the hundreds chips. Without looking, have students drop out a few chips and determine the total value of the number spilled from the cup. Then, have students pour out more chips and determine the total value of that stack of chips. Have students use the chips to add the two values together. Repeat and discuss what to do when there are more than 9 ones, tens, or hundreds.

I introduce the concept of regrouping with snap cubes. I give students any 2-digit number and 1-digit number that require regrouping. Students should use the snap cubes to build the 2-digit number on the place value mat. Then, students should add the one-digit number to the addend. Students must fill up the first ten frame before beginning a new ten frame. After students add the ones, ask if they are able to regroup and replace ten ones for a ten.
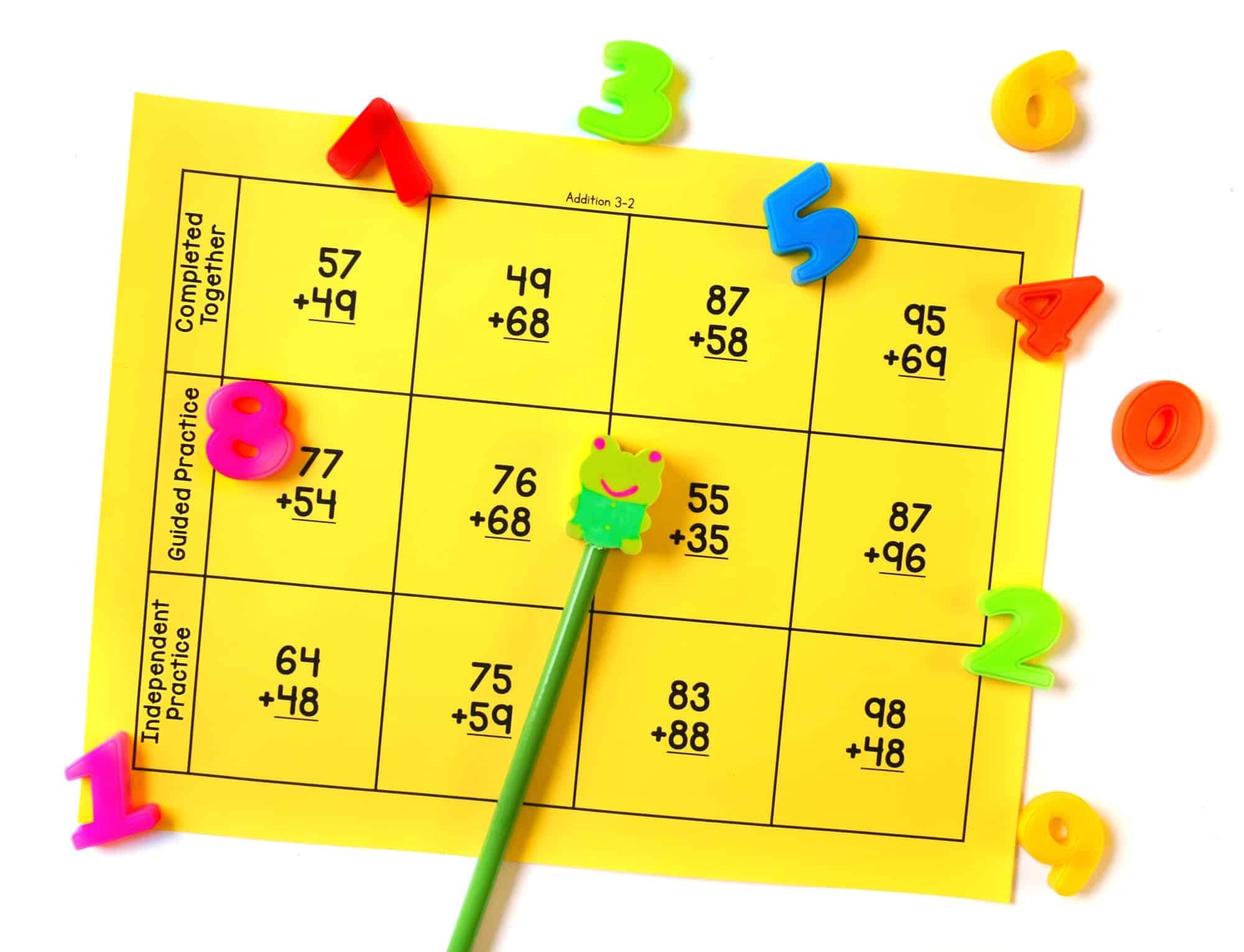
Even though the focus of these lessons is the concept of addition, I feel like I would be remiss in not including the addition algorithm, so I added a week specifically designed for the addition algorithm. I included one day for 2-digit plus 2-digit problems and each day I add an extra digit to the algorithm. If your school/district/state doesn’t want the algorithm taught, then you can certainly skip over these lessons.
You can access all of the lessons in this post here.
You can learn more about the math interventions here, and you can see a place value focused post here.


