Teaching fractions greater than one (mixed numbers to improper fractions) shouldn’t be an isolated part of your fraction unit. Instead, fractions greater than one should be embedded in your fraction instruction. This post includes some of my favorite lessons for teaching mixed numbers to improper fractions (and the reverse).
Fractions Greater Than One
For instance, in the lesson below, students determine how to slice and share pizzas. In some problems there are more children than pizzas (six children and four pizzas), so the fractional amount each child will get is less than one whole. In other problems there are more pizzas then children (three children and four pizzas), so the fractional amount each child will get is greater than one whole. I don’t explicitly teach fractions greater than one prior to this lesson. Instead, I let students discover their own way of solving the problem.
At the conclusion of the activity, I have students share different responses. For the four pizzas and three children problem, some students may say one and one third pizza and other students may say four thirds. I bring that to the class’s attention and let them debate on which response is correct. This lends itself into me introducing the terms mixed numbers and improper fractions.
I use the following lesson to further develop this concept. Students determine if each fractional amount is greater than one. If the fraction is greater than one, students write the fraction as a mixed number and an improper fraction.
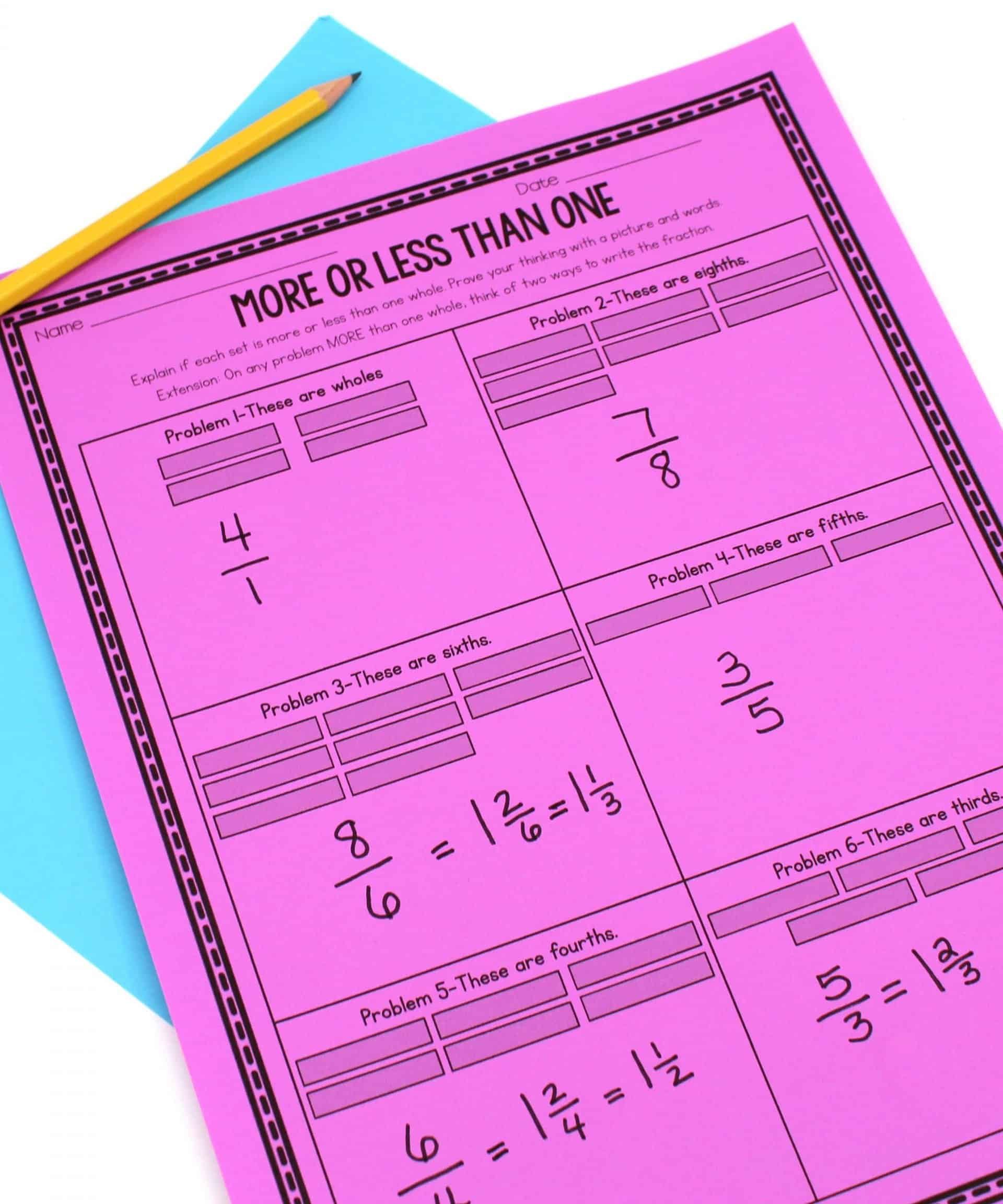
I do share that there is considerable debate over the appropriateness of referring to improper fractions as “improper” and let students chime in on the debate.
Mixed Numbers to Improper Fractions
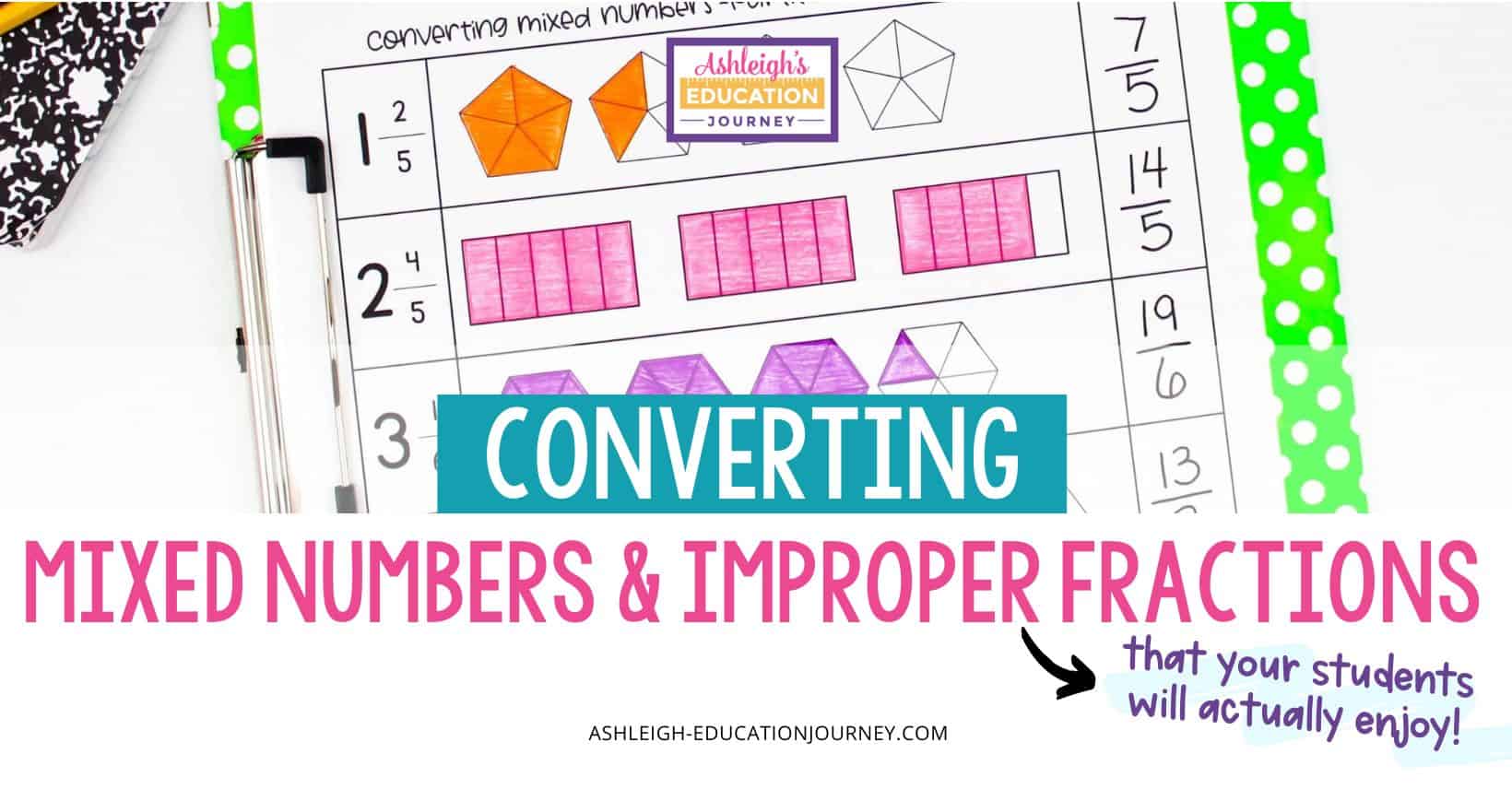
Students tend to have some difficulty converting fractions greater than one to mixed numbers or mixed numbers into improper fractions. I like to give students plenty of practice with visual representations. When this practice, students begin to see they can divide the numerator by the denominator to convert to a mixed number, and they understand WHY it works.
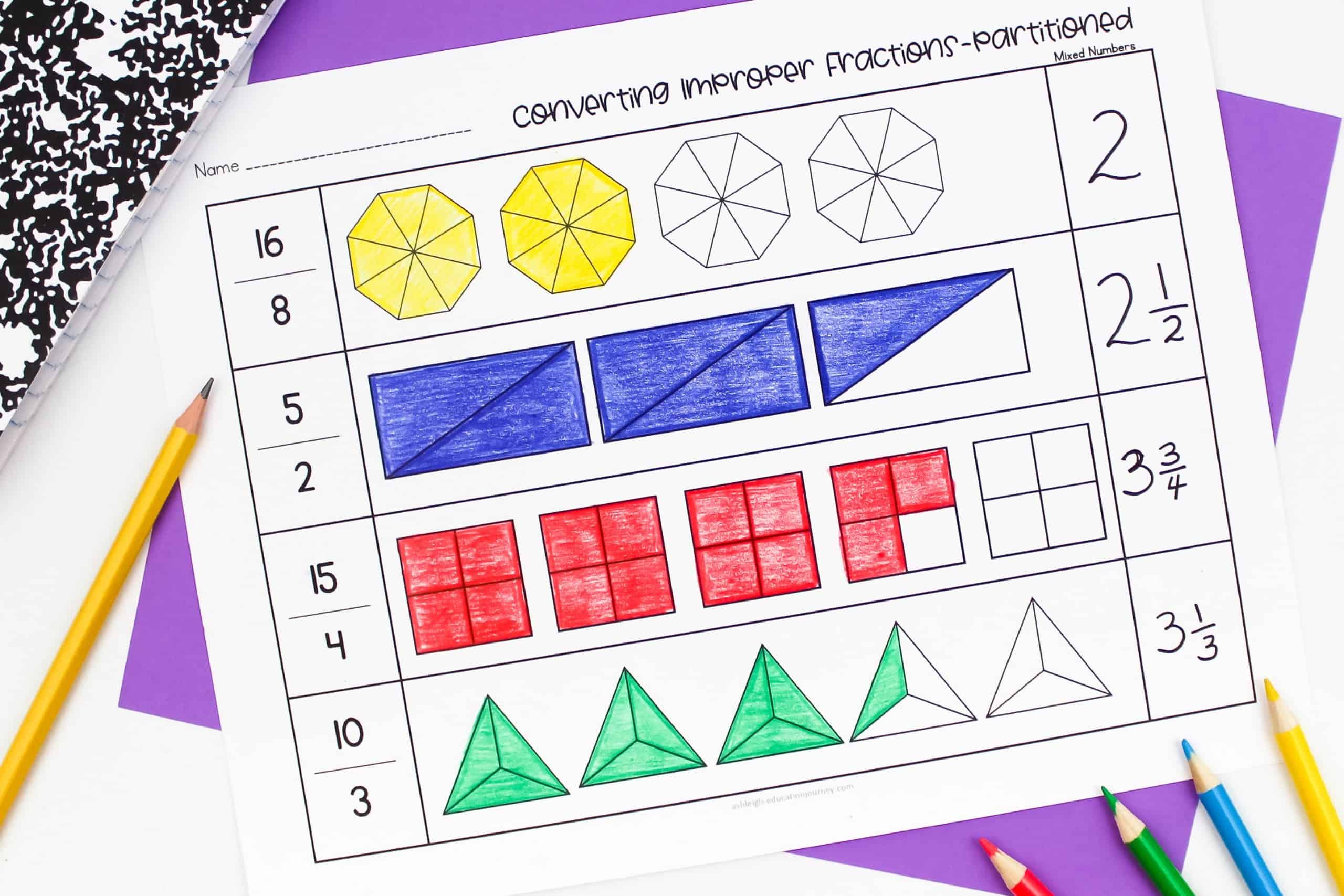
The reverse is also effective. With visual representations, students learn to multiply the whole by the denominator and add the numerator to form an improper fraction. As with most fraction concepts, I try to let students discover them for themselves during their work time and we discuss the strategy during our closing.
As students become more comfortable with converting mixed numbers to improper fractions, I remove the included partitions in the shapes and have students partition the fractions on their own. This adds an additional layer of understanding and challenge.
It’s important to incorporate fractions on a number line frequently, so students can use number lines to convert fractions greater than one.
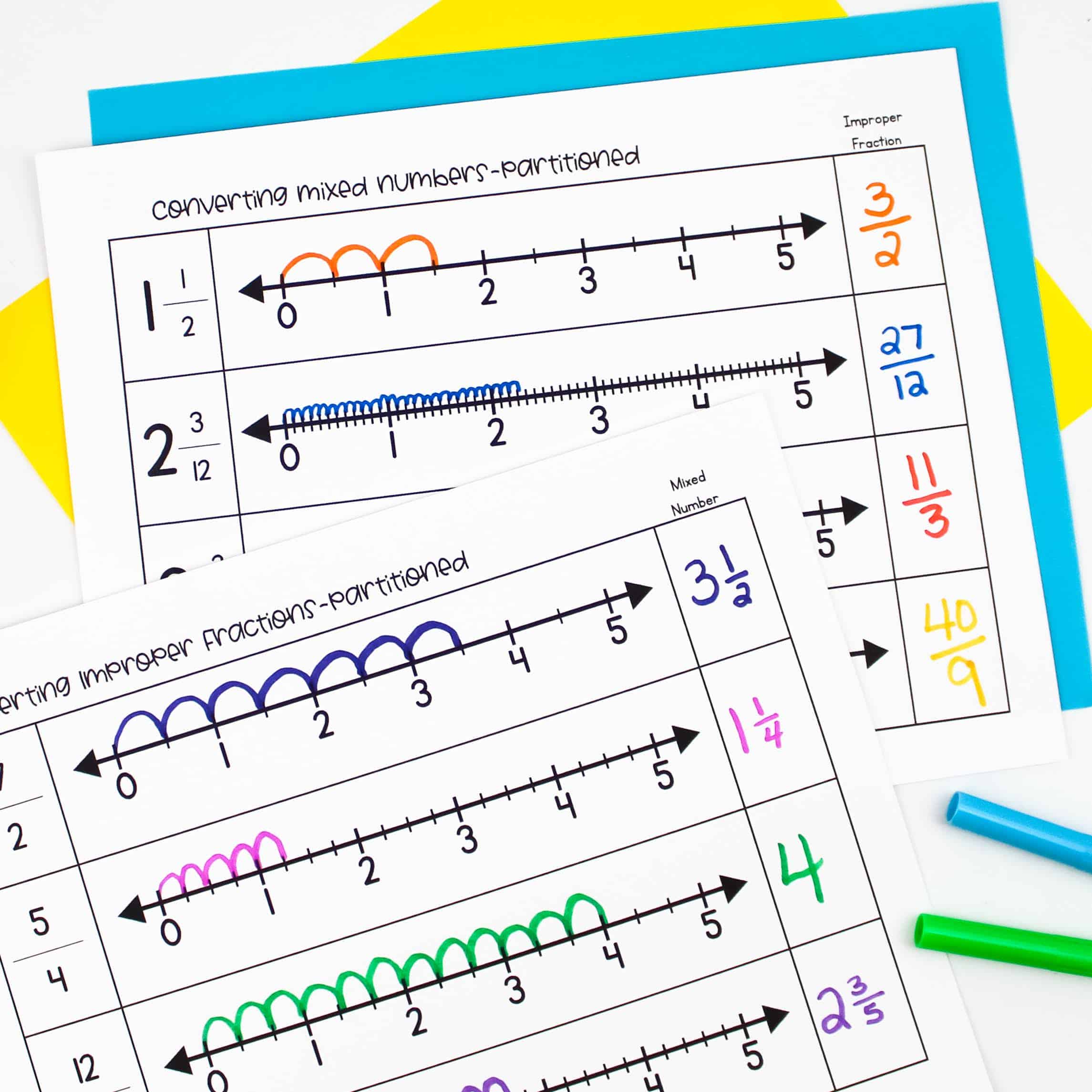I recommend reviewing this frequently, because I’ve found that this is the one fraction skill students are most likely to forget. Because of the speed we move through our standards, some students may eventually confuse this with other fraction concepts.
When teaching converting mixed numbers to improper fractions, be sure to include problem solving tasks, such as the one below. In this lesson, students determine the value of each pattern block. That’s not quite a challenge when the hexagon represents the whole. But, things change when the whole changes to the trapezoid, rhombus, and the triangle.
You can find all of these mixed number to improper fraction lessons here! If you’re looking for more, or different, ideas for teaching fractions, don’t skip this post! It is packed with great content.
