Teaching Decimals

Like fractions, introducing decimals is something that should be taught for deep conceptual understanding in order for students to be successful in high level math classes. It can be easy, even tempting, to breeze through a decimal unit, but students need plenty of opportunities to explore decimals with manipulatives and pictorial representations, and reason with the size and value of decimals in order to develop an authentic understanding. The lessons below can be found in my decimal unit here; even if you don’t use my unit, hopefully you’ll find plenty of ideas you can try out!

I always begin my unit on introducing decimals after I teach place value and factions, since those concepts lay the foundation of the decimal unit. When I begin the unit, I revisit the concept that the value of a digit is ten times greater in the place to the left. I also teach students that the value of a digit is ten times less in the place to the right. Once we begin talking about ten times less, I ask students to share another way to represent ten times less, and have students recognize that they can say one-tenth the size of the digit to the left. We use our place value pockets for hands-on practice.

I teach my students the role of the decimal point, which is one of the most important lessons of my decimal unit. I use a document camera to show that the 10 to 1 rule continues indefinitely to larger and larger numbers. Then, I ask students if there is ever a smallest piece. To illustrate this, I pass out the ones pieces and explain that the squares represent one whole. I ask students if I can divide my one by ten to have an even smaller piece and help students realize that a one could be divided into ten smaller strips by having students divide their ten into ten equal pieces. Students should think of a way to write that number as a fraction. Then, I ask if it is possible for to divide our tenth by ten to have even smaller pieces. Students should think of a way to write that number as a fraction. I use this opportunity to introduce the decimal point and explain that a decimal point is placed between two positions, and the position to the left of the decimal point of the ones position. The role of the decimal point is to designate the ones position.

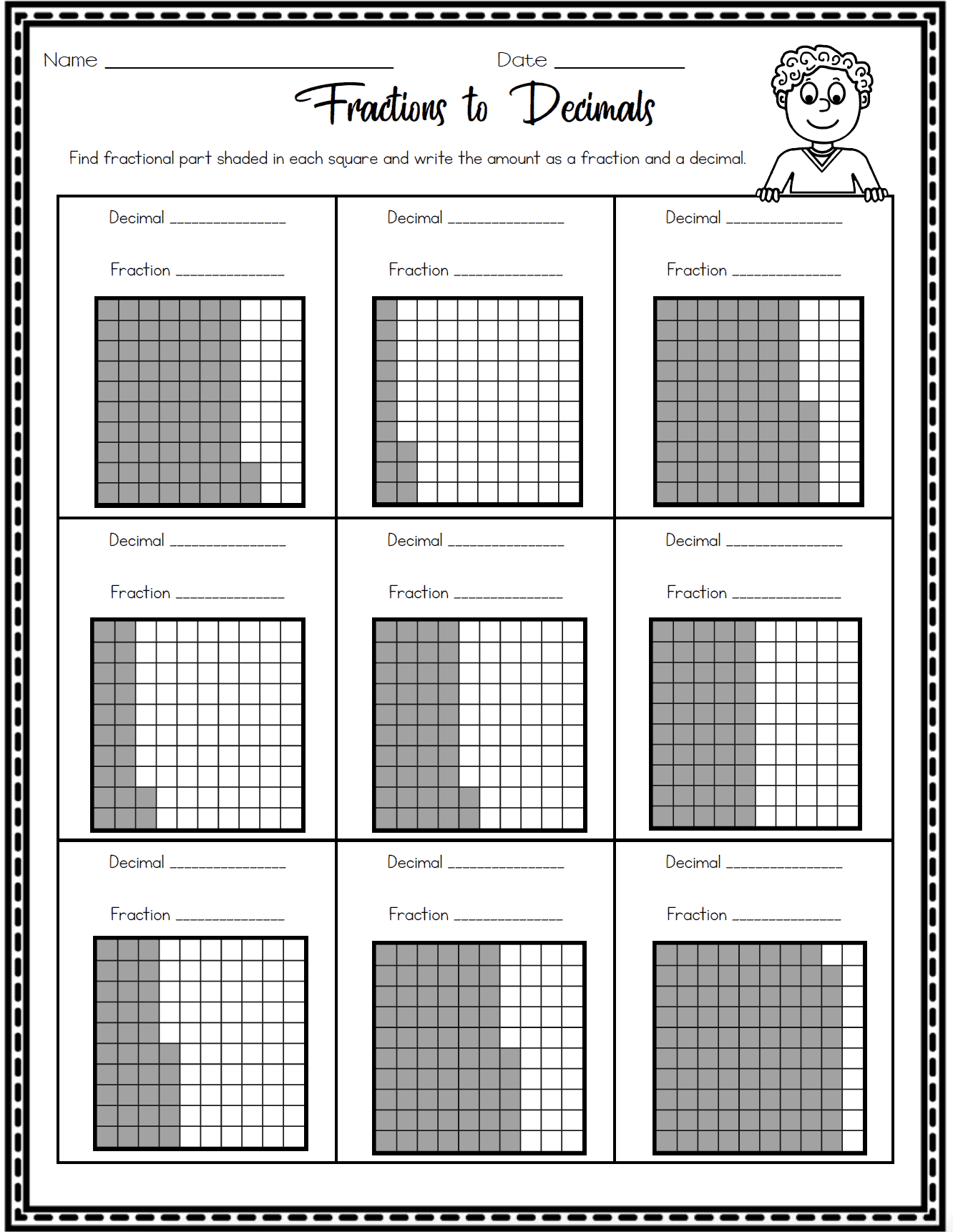
In my following lesson, I teach students how to represent fractions as decimals using pictorial models. At this point, I only use models with a total of 100 or ten, which is typically easy for most students.

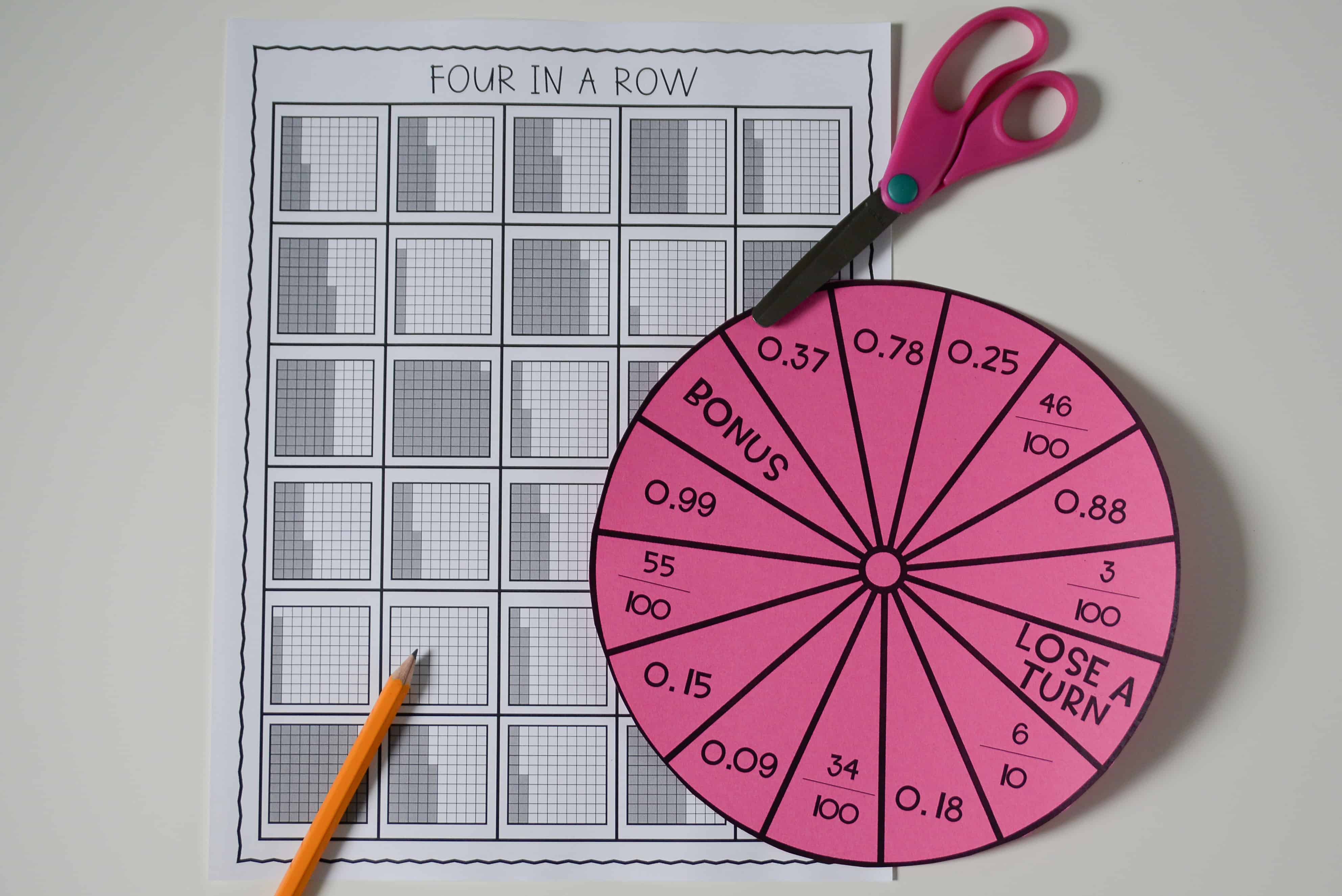
I reinforce that with games such as Four in a Row, where students see who can shade four in a row first. Students spin the spinner and find a model that represents the fraction or decimal that the spinner landed on. The student will cover that model with a counter. Then, their partner will repeat the steps above and cover his/her model with a different color counter. Students repeat these steps until there is a winner.

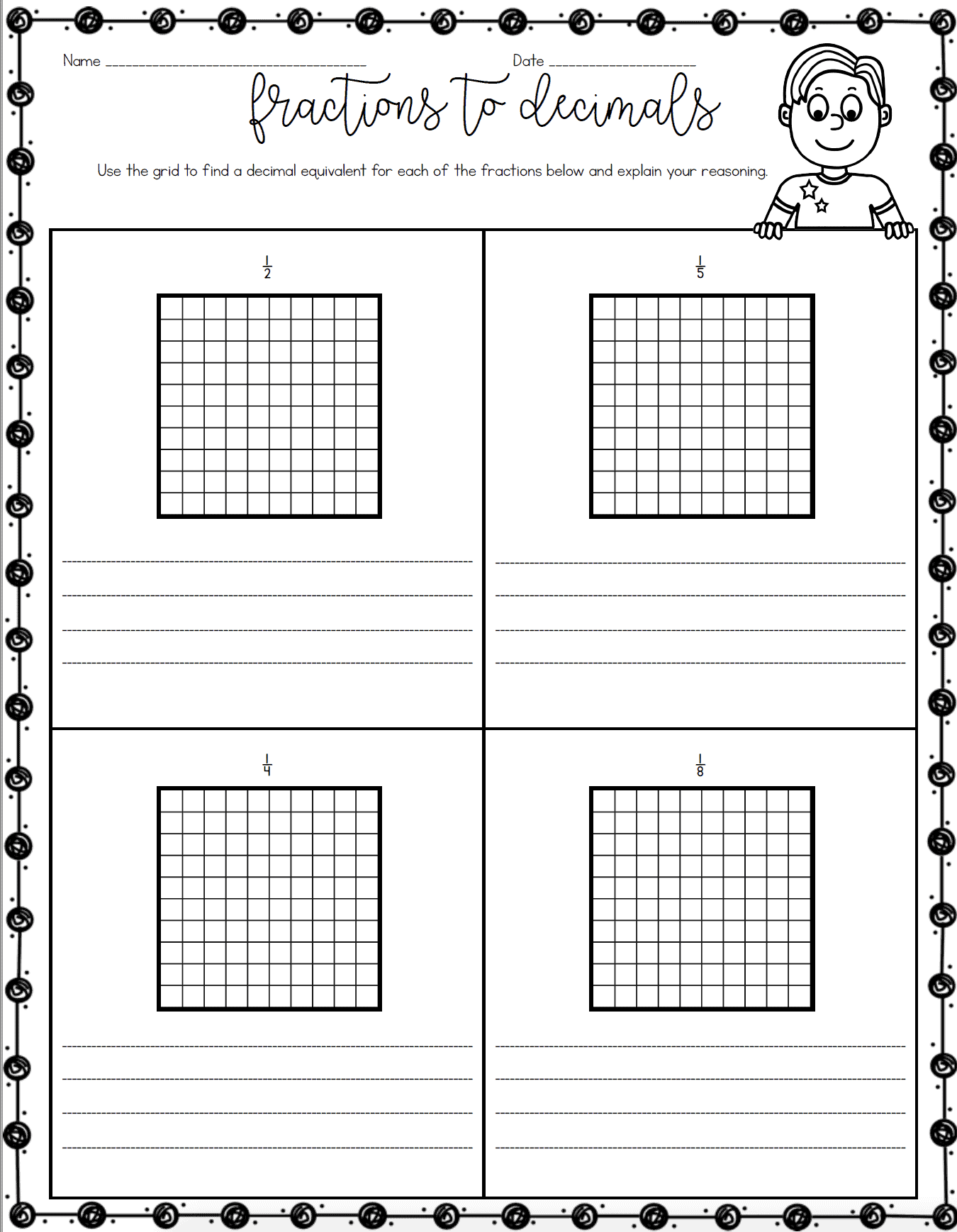
I then teach students how to write a decimal as a fraction. Rather than giving students a pictorial representation, I have students create a pictorial representation for each decimal or fraction.

 

As I teach students how to write decimals as fractions and how to write fractions as decimals, I begin giving students more challenging problems. This requires students to think more deeply about the relationship between decimals and fractions. For example, students problem solve to realize that one-fourth is the same as 0.25.

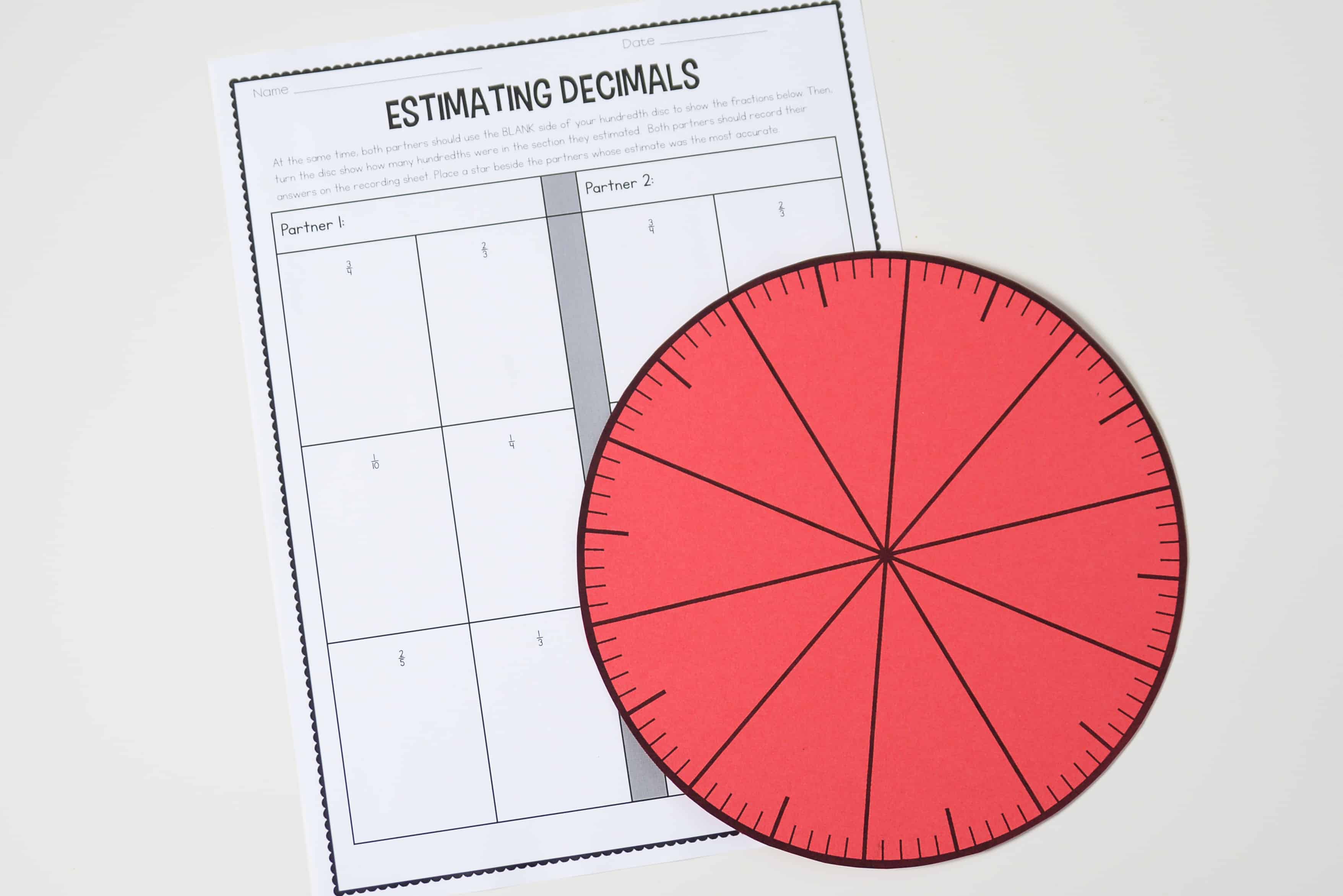
To deepen students’ number sense, I also have students estimate with decimals. One great way to do this is with a highly underused math manipulative-a hundredth disc. In this activity, students use the hundredths disc to build the fractions shown on the recording sheet. They should then use the hundredth disc to find the equivalent decimal.

I also teach students to mark and identify decimals on a number line. In the activity below, students cut out the squares to make two numbers lines to represent the decimals. We also do more general practice where students identify the point on a number line.

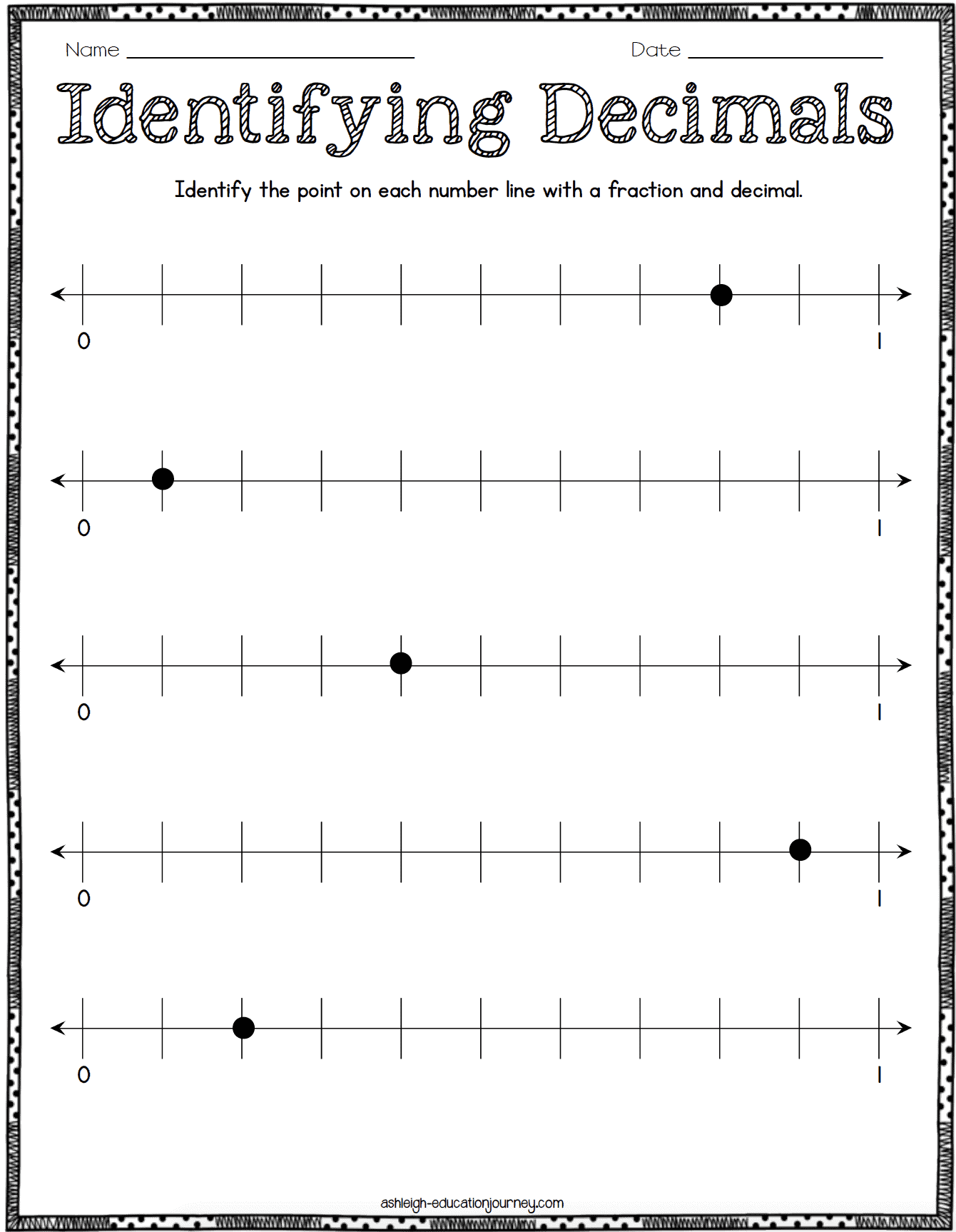
Once students have a firm understanding of decimals, I begin introducing friendly numbers by relating decimals to friendly fractions. For example, students may have to explain what friendly fraction 24.82 is closest to. In this activity, there is not necessarily a right or wrong answer. Instead, these open ended questions allow students to have high levels of math talk where they may disagree with each other and try to justify their reasoning. We also complete an activity where students receive ten decimal and fraction cards and must determine which cards make the best match. This is another open ended task that encourages high levels of thinking and a written explanation of student thinking.

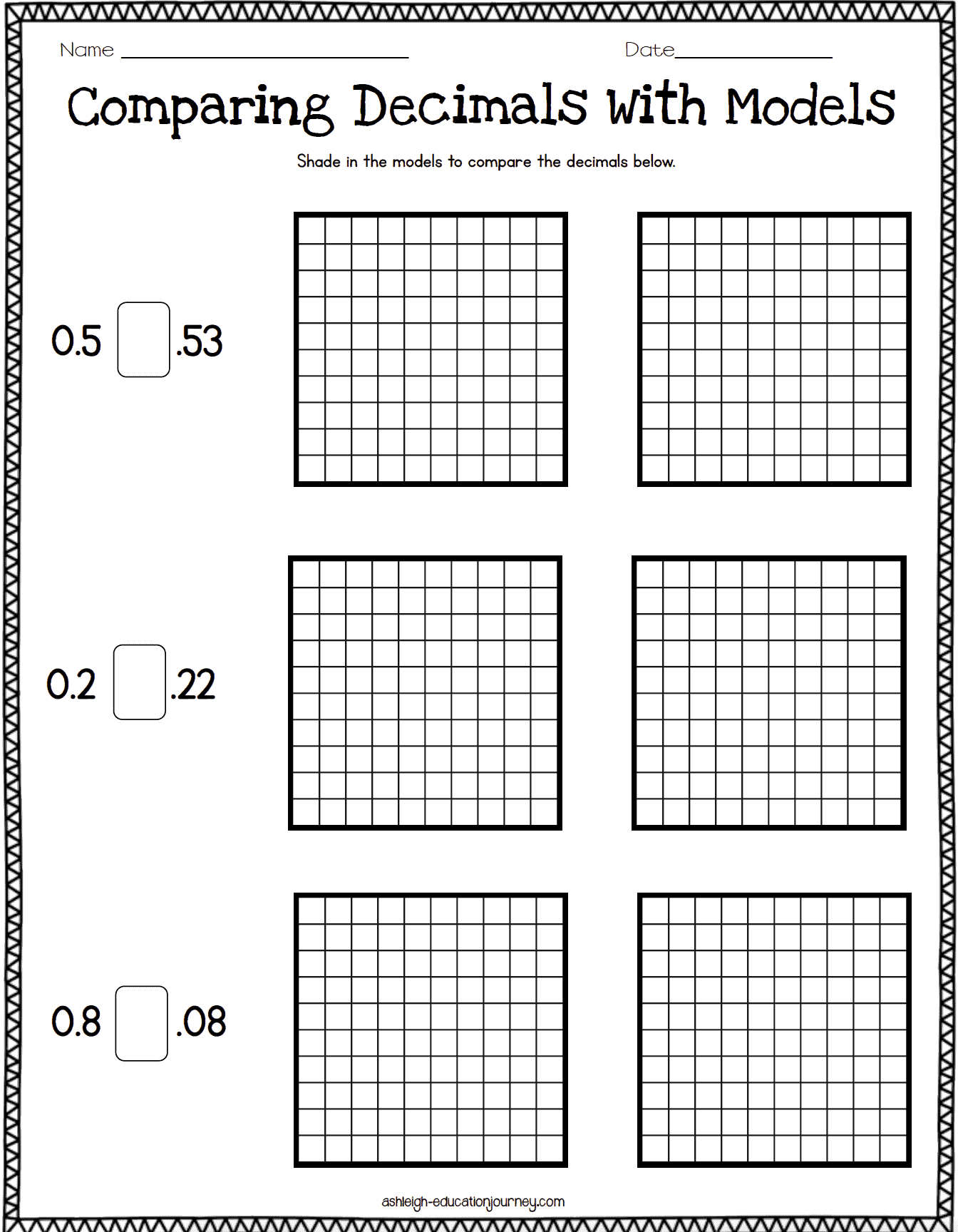
As I teach about the size of decimals, students use models to compare decimals. I eventually take the models away and have students compare decimals without models. Another way students practice comparing decimals is through the card game of War. Students have cards with many different representations of decimals. They shuffle the cards and place them face down. Partners take turn drawing a card and whoever has the card with the greatest value gets to keep both cards.

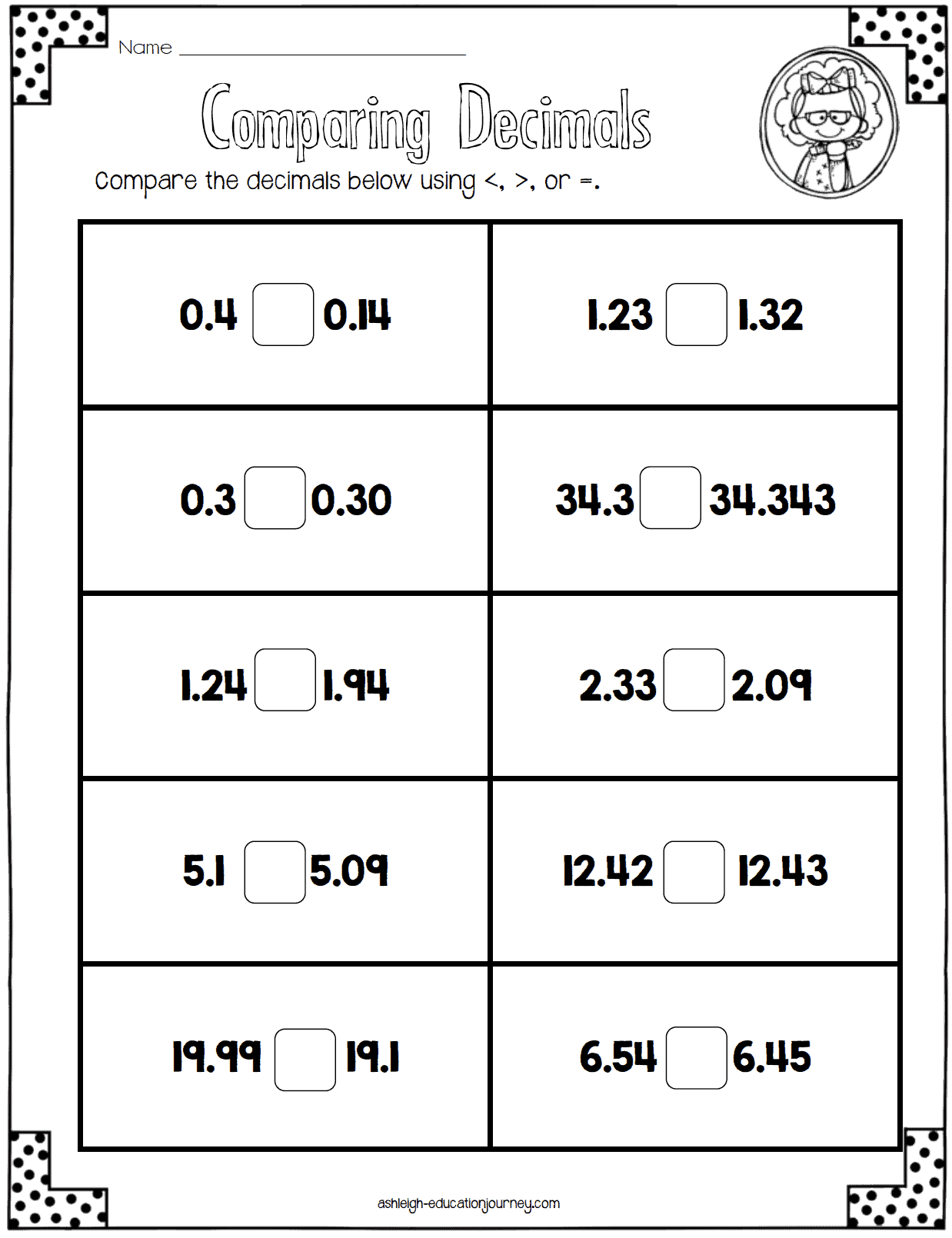
I also teach Nice Numbers, which is essentially rounding decimals. I give students two decimals and they determine which whole number or which tenth the number is closest to.

Toward the end of my decimal unit, I teach students to add and subtract decimals and fractions with denominators of ten and one hundred.

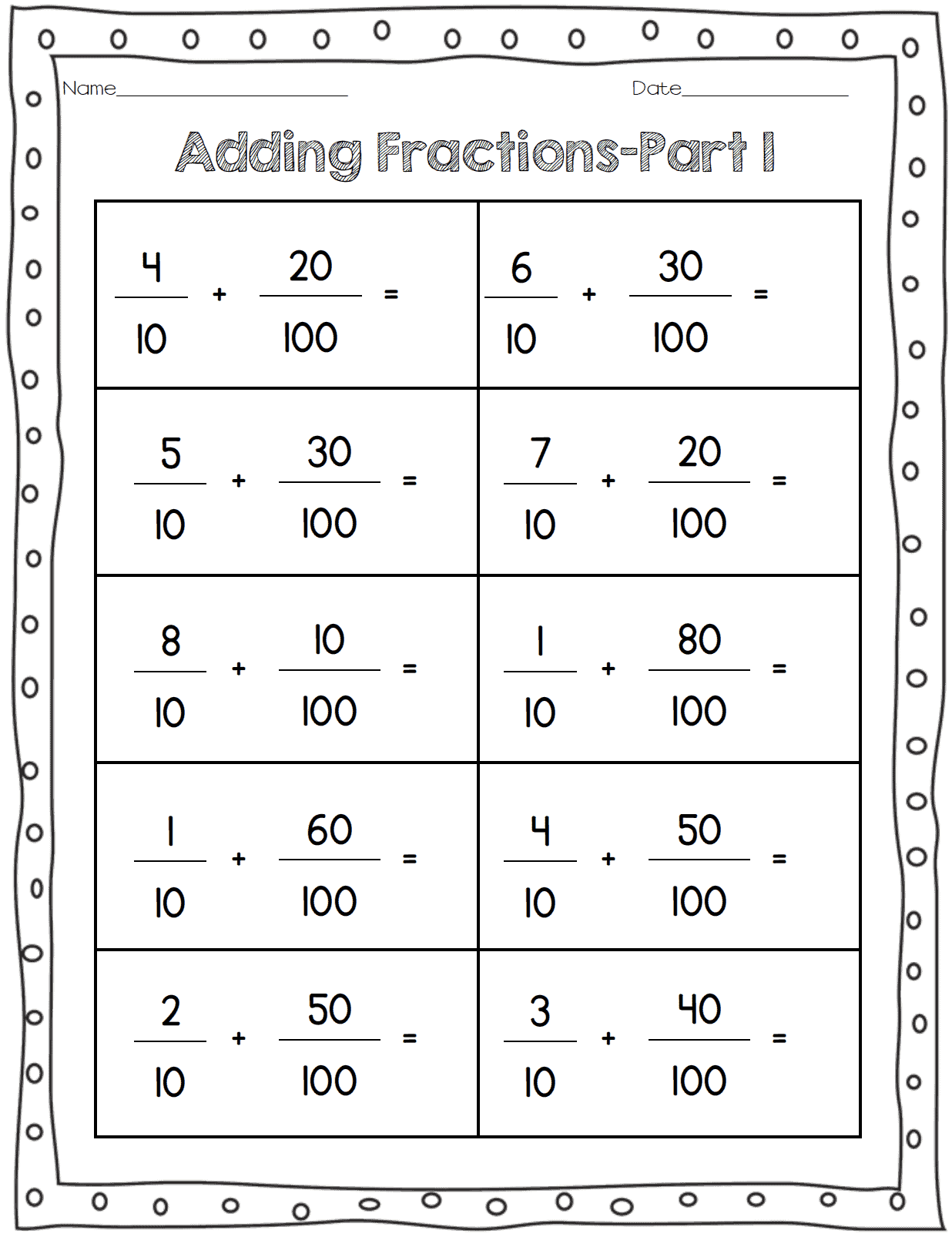
I love incorporating art and decimals with this Decimal Pictures activity. To keep this activity challenging, it’s important for students to NOT color the same number of squares each color. I like to have students cut out the square and mount both papers on black construction paper for a hallway display.

We end the unit with about a week’s worth of problem solving tasks involving decimals. I feel that it’s essential for students to apply what they’ve learned in real-world problem solving applications.

 

Conclusion

I love how decimals build upon fractions and decimals and connects so many different concepts together. Anytime I can connect topics and concepts, I feel that students gain a much better understanding.  I also wanted to post a couple of pictures of a really fun decimal activity that my students recently completed.  It was super quick and easy to prepare for, but my students really enjoyed it.  All you really need is a circle divided into 10 equal pieces for your students.  At first, I tried having my students draw their own circle and dividing the pieces themselves, but that was pretty much a disaster!  I could barely do it myself!  I finally just printed a circle out, and that made it MUCH easier.  As a class we customized our own special pizza (see chart below).  We chose a variety of toppings and decided what tenth of our pizza should have each of the toppings. Students then decorated their pizzas to reflect the toppings/decimals.

One clarification I had to make with my students is that the decimal (for instance 0.4) does not mean there should be 4 pieces of sausage on each slice.  It means that 4 of the slices should have sausage.