
Rather than titling this post “Teaching Fraction Sense”, I might should have titled it “Teaching FOR Fraction Sense” as it’s not something that is taught in a few fraction lessons. Instead, it has to be developed over time.
Number sense has become a critical topic among elementary math teachers. However, the importance of number sense doesn’t stop after the primary years, and it doesn’t stop with whole numbers. Our students must also extend their existing number sense into fraction sense.
When students build on their current number sense, they relate what they know about whole numbers to fractions. This generalization both helps and hurts students as they work with fractions. For example, students may see the numerator and denominator as separate values, rather than one number. A common challenge is when students view fractions such as 1/3 as smaller than fractions such as 1/8, because three is smaller than eight. Other misconceptions arise as students begin computation with fractions.
Students need time to develop their fraction sense. However, there is never enough time in the year to teach our math standards. While, I don’t see that changing anytime soon, one way to support fraction sense (and number sense) is through math warm-ups. I won’t go into great detail on early numeracy concepts, you can read more about that here. In this post, I’ve shared how I use math warm-ups to develop these same concepts for fractions.
Fraction Sense – Subitizing
Subitizing is the ability to instantly recognize an amount. This is typically done with dots in grades K-2, but students can also subitize fractional amounts. Students should be able to tell what fraction is shaded (and not shaded) without counting.
When completing this activity, show students an image for a few seconds and have students try to determine the quantity shown. After showing the image, have students share the quantity and record their responses. Once students share their quantities, show the image again for verification.
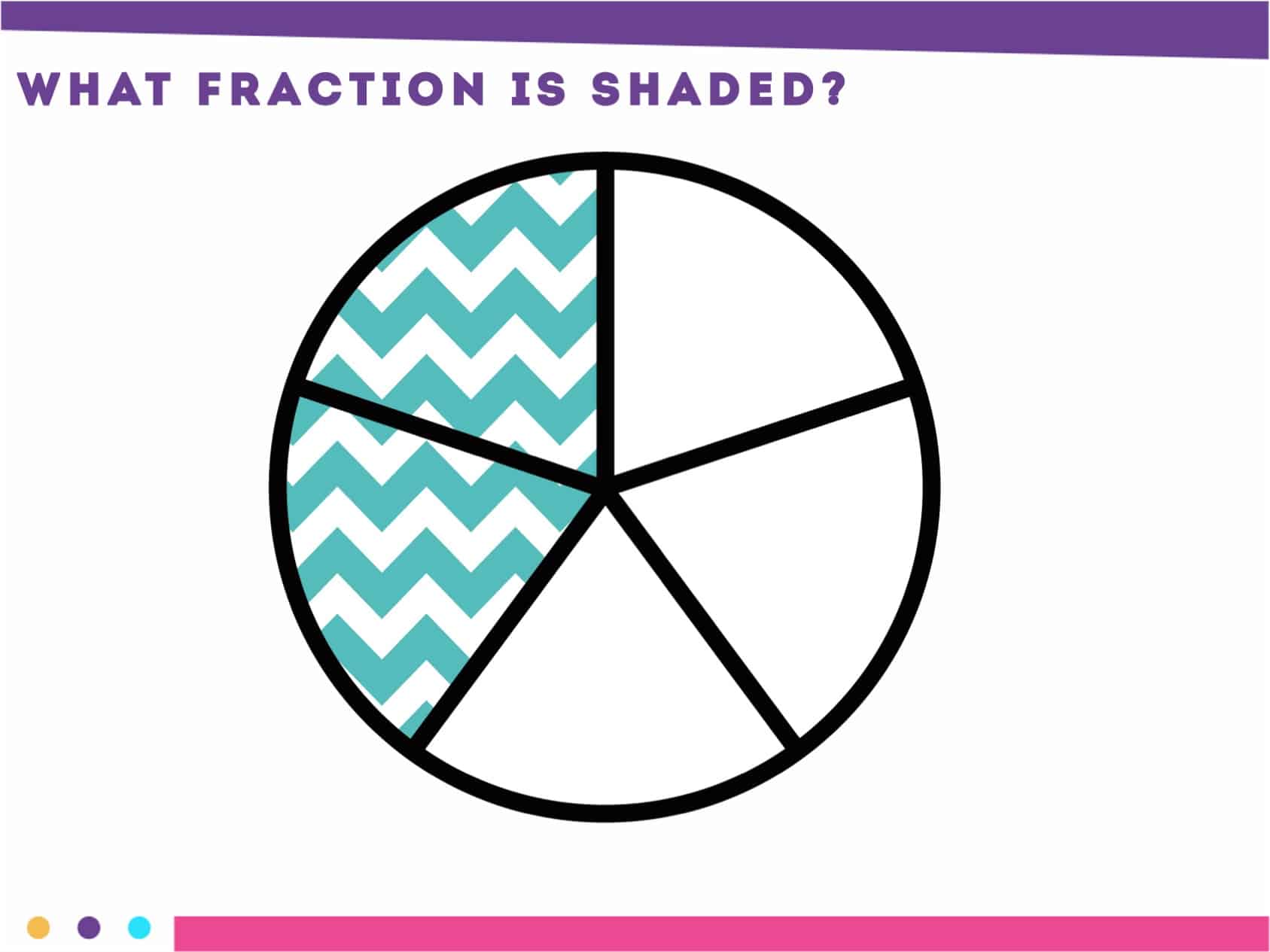
When completing these activities, avoid working with large denominators. I wouldn’t recommend anything higher than five or six. I also do not use fractions in a set for this activity.
Fraction Sense-Verbal Counting
Verbal counting is exactly what it sounds like-counting out loud and in order. This is essential for developing fraction sense.
One of my favorite strategies for verbal counting is through a count the room activity. Each child says a number as students count one-by-one around the room. To teach the procedure for this activity, start with simple numbers and sequences, so you can focus on expectations and procedures. This does work best with students sitting in a circle, but as long as students know the order in which they are counting any seating arrangement will work.

If students can’t count with fractions, it’s really hard to solve operations with them. Students learn to add and subtraction whole numbers based on counting, and it is how most students learn to add and subtract fractions. As students count by fractions, you can record the number or display the fractions digitally as shown below.
One/Two More/Less
This is another activity that teachers spend a lot of time on with younger students. It’s no surprise that students need this for fractions as well. You can complete this with fraction images of fractions and numerical representations of fractions.
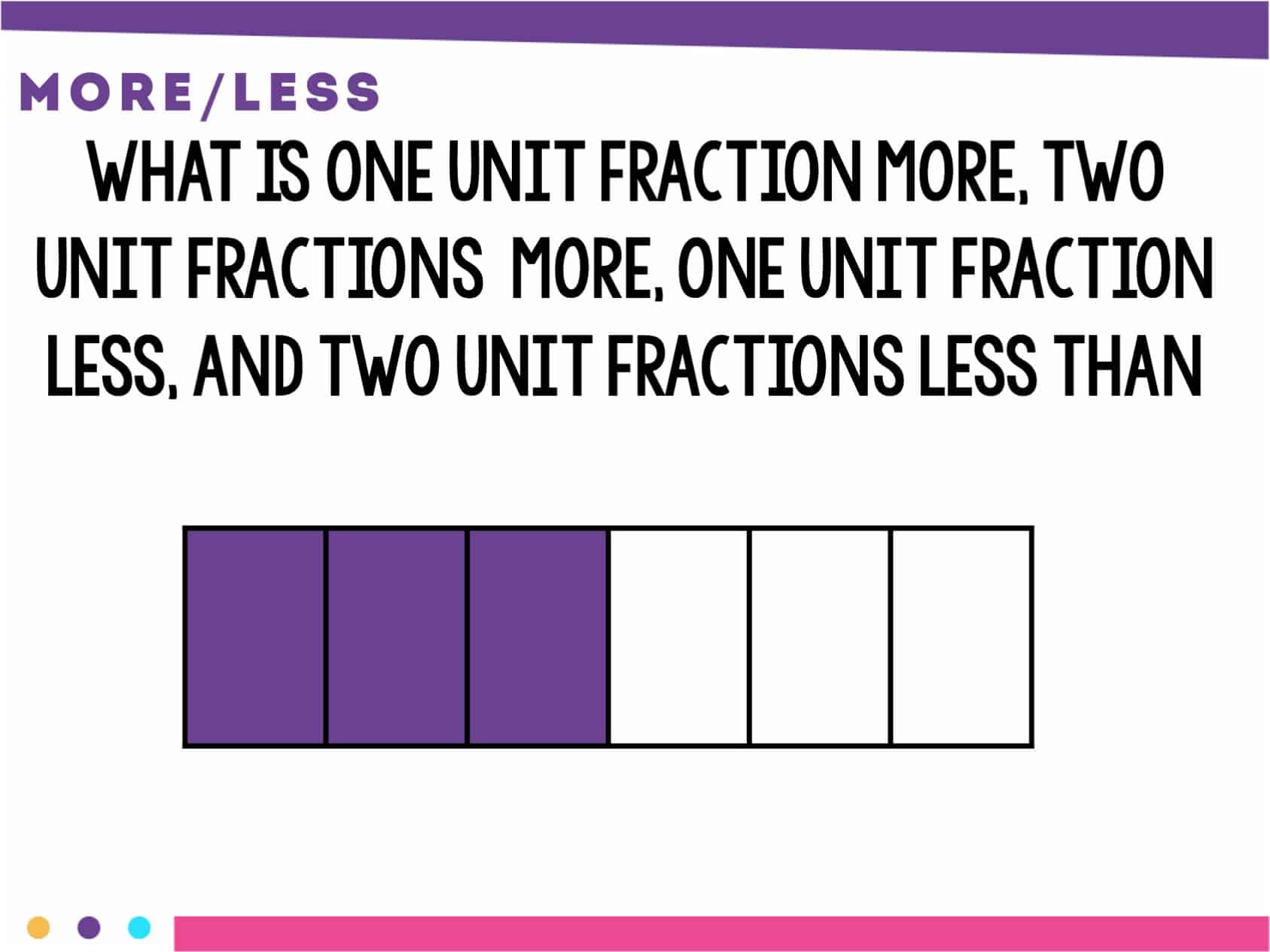
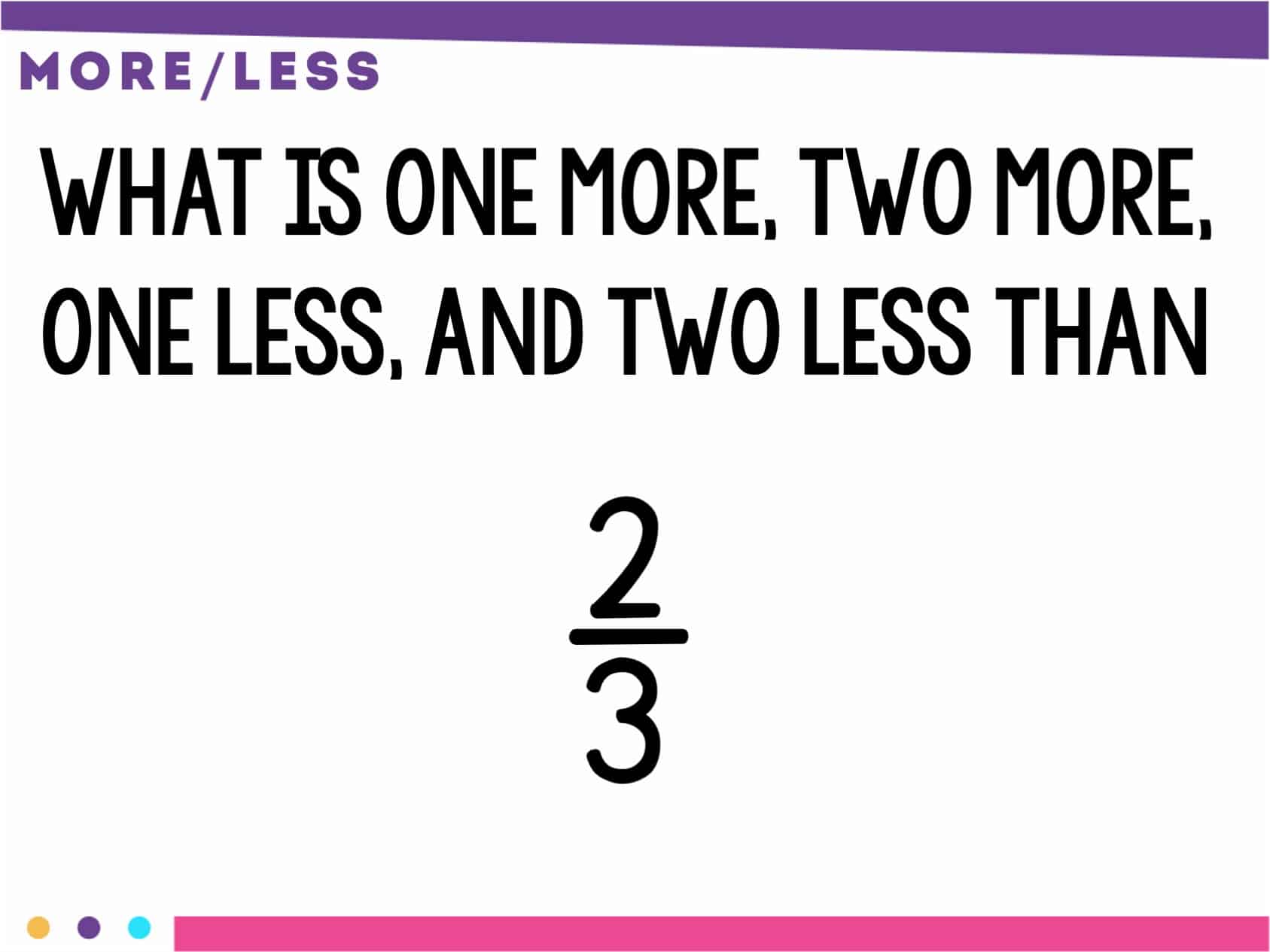
You could even ask what is one whole more (or less if possible). Now that I implement this routine, I rarely ever have students try to add or subtract the denominators. They have realized that the size of the pieces does not change, just the amount of the pieces.
Which One Doesn’t Belong
When developing fraction sense, students need experiences comparing groups of items by looking at similarities and differences. Christopher Danielson wrote the book Which One Doesn’t Belong and has further developed the idea on his blog. In this routine students are asked to look at four images or numbers and determine which one doesn’t belong. Of course, students must also share their reasoning. Students love this routine because there are no wrong answers, as long as the student can justify his/her reasoning. The focus isn’t on the answer, as much as on the student being able to communicate his/her justification of their selection.

Steve Wyborney has developed one of my all-time favorite math warm-up activities. He has a huge collection of free activities on his website. In the activity, I first show students an image and ask what value the image represents.
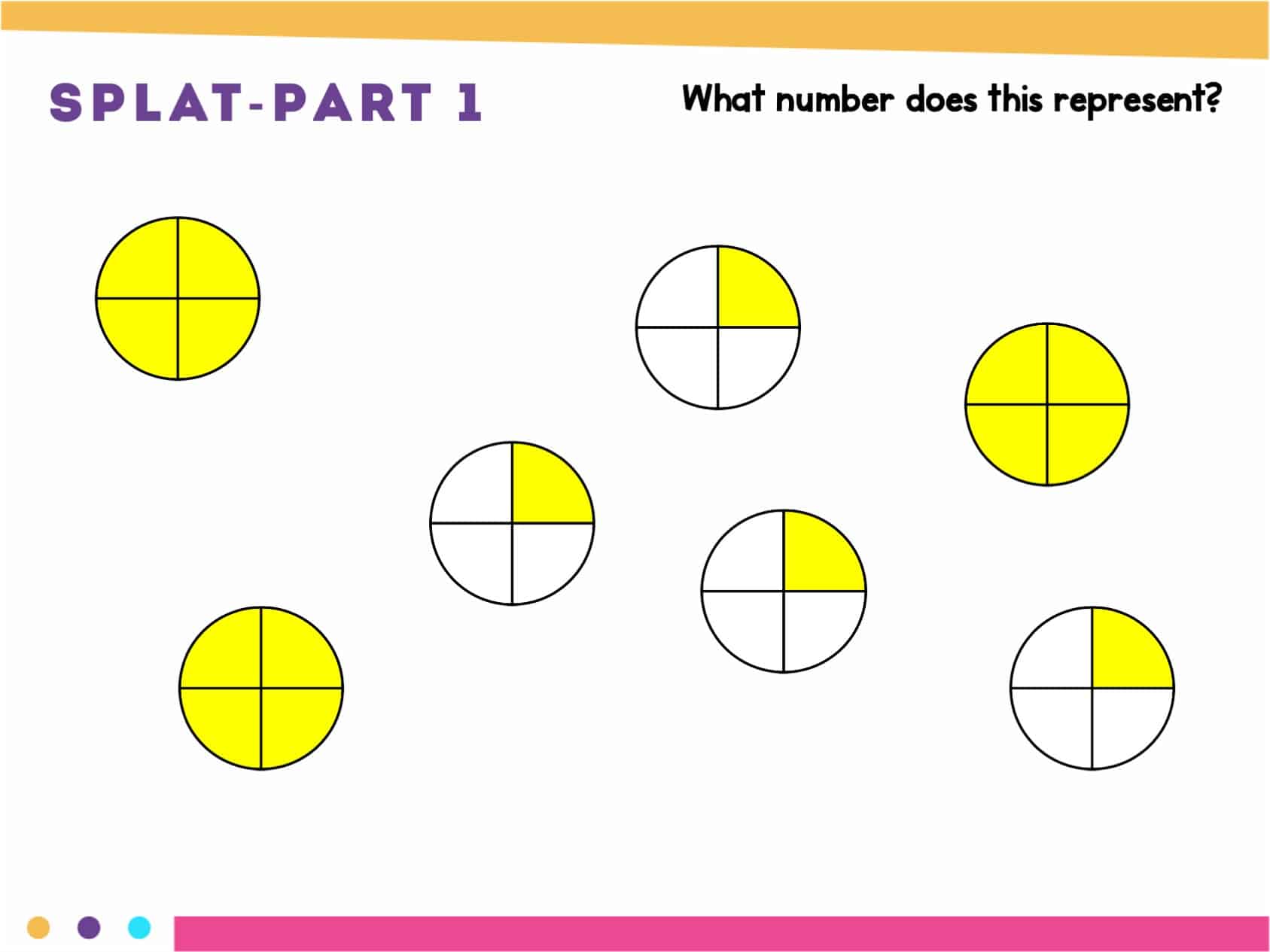
Then, an unknown amount is covered (with paint, slime, something else???). Students determine how much was covered by the blob.

Finally, the blogs become translucent so students can validate their responses. Students love the activity, and I love how it engages their thinking as they develop their fraction sense.

Benchmark Fractions
In this activity, choose a mystery number, but do not tell students the number. Show students a number line with two numbers that are at the endpoints and place a question mark on the mystery number’s location on the number line. Then, have students try to guess the mystery number. After each guess, record the number they guessed where it lies on the number line.
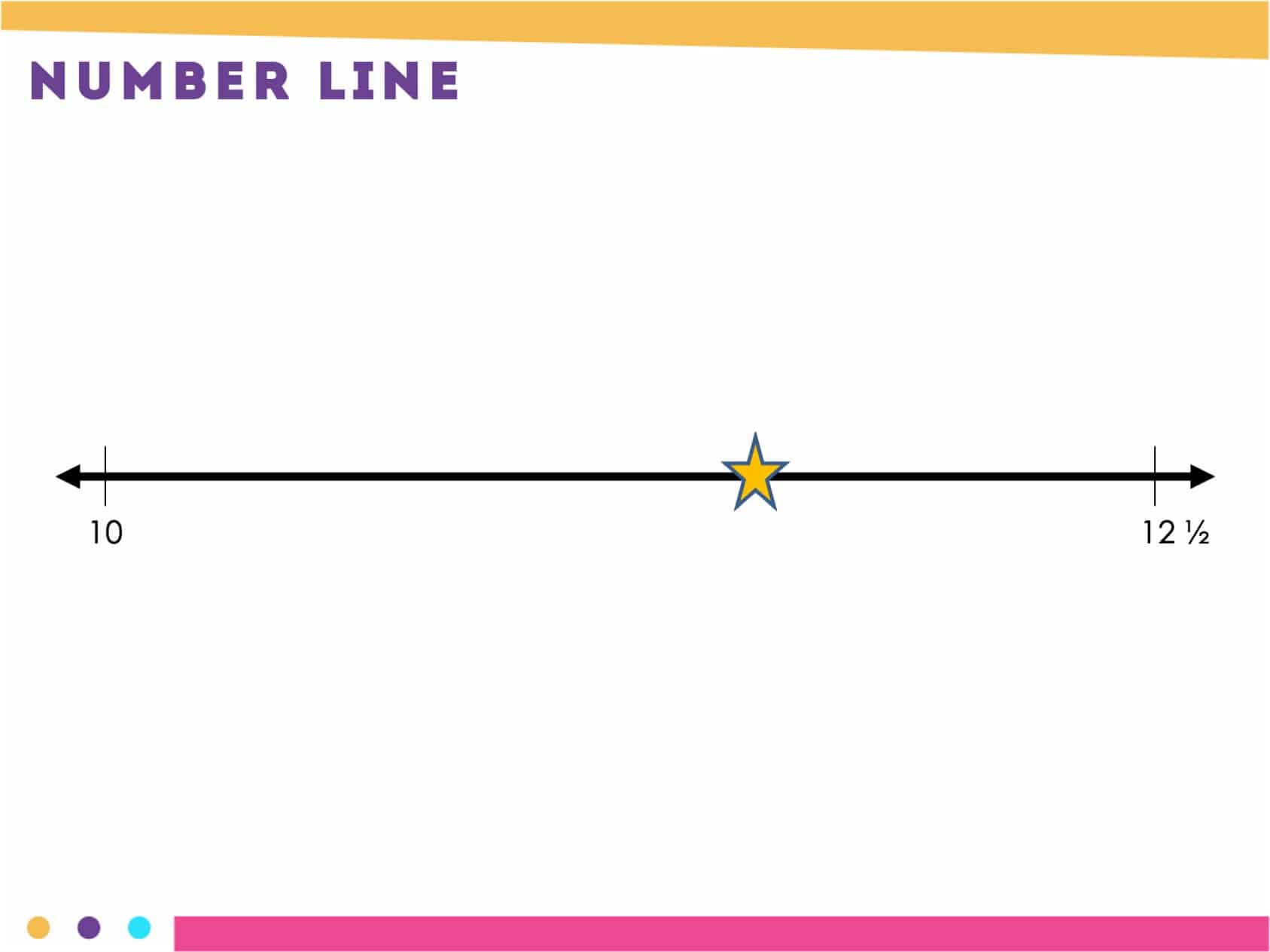
The activity provides students with the opportunity to think about the size and relative location of numbers. It’s also a great way to encourage students to think about benchmark numbers.


