
These number sense routines can be a game-changer for your students. Last year, I wrote a blog post solely dedicated to teaching number sense. That post shares a more general overview of what number sense is and why it’s important. This post moves directly into ways to improve students’ number sense. I’ve shared some of my favorite ways to use math warm-ups to develop and improve upper elementary students’ number sense. You can find the lessons here.
As an upper elementary teacher, it’s easy to identify students who lack number sense. Unfortunately, it feels like the quantity of students lacking number sense is increasing every year, and it makes teaching advanced math concepts incredibly difficult. Without number sense, it is difficult for students to compute and to find relationships within numbers or equations. In fact, most common error patterns point directly to a lack of number sense. This is also one of the primary reasons students struggle with problem solving, as students solve problems without finding meaning or making sense of the question.
Number Sense Routines
The good news is that none of the number sense routines below require any prep. If fact, simplicity is the name of the game. There’s no need for elaborate set-ups or fancy materials. Students gather together as a whole group (virtually or in-class) and complete one number sense activity a day.
Once students are gathered, display the problem of the day by opening the included link that takes you to Google Slides. You can also display the PowerPoint version of the file, whichever works best for you! If you use the PowerPoint version, it is important that the problem is displayed in slideshow mode, because this will allow the transitions to display appropriately.
The power in these lessons come from the class conversations, so this is not something that can be completed independently. Students need to share and discuss their thoughts and the conversations will definitely need your guidance.
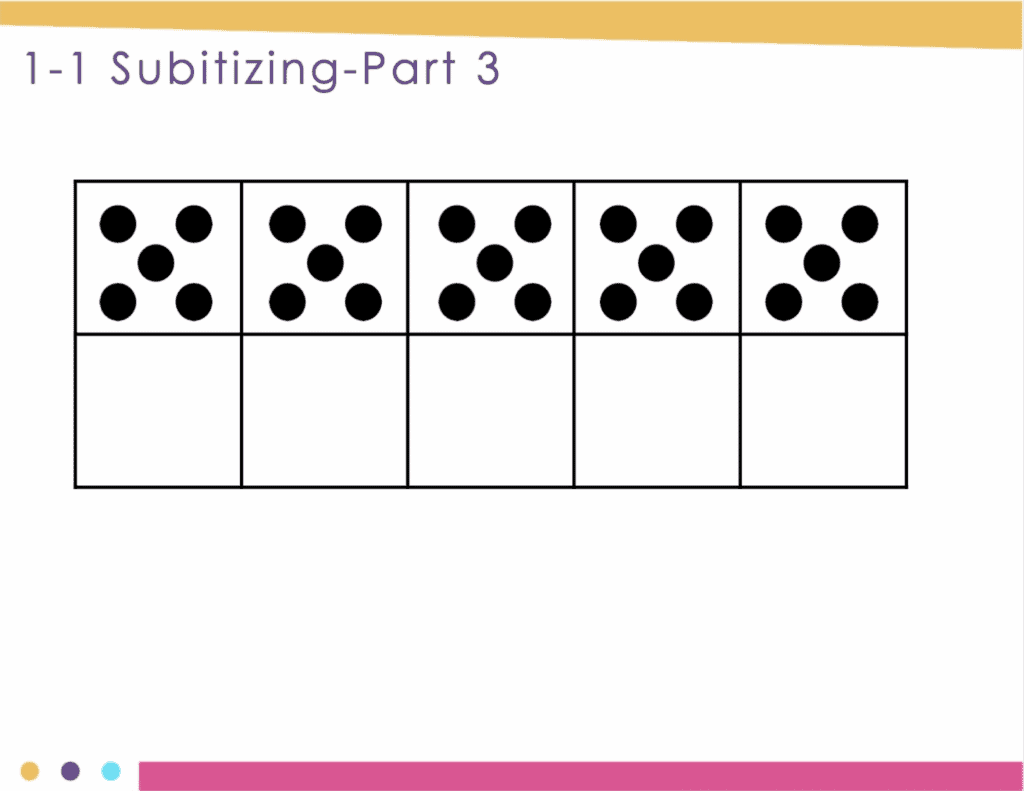
Number Sense Routines – Quick Images
Quick images are pictures of quantities that are organized to encourage subitizing and unitizing, and they are the perfect addition to your number sense routines.
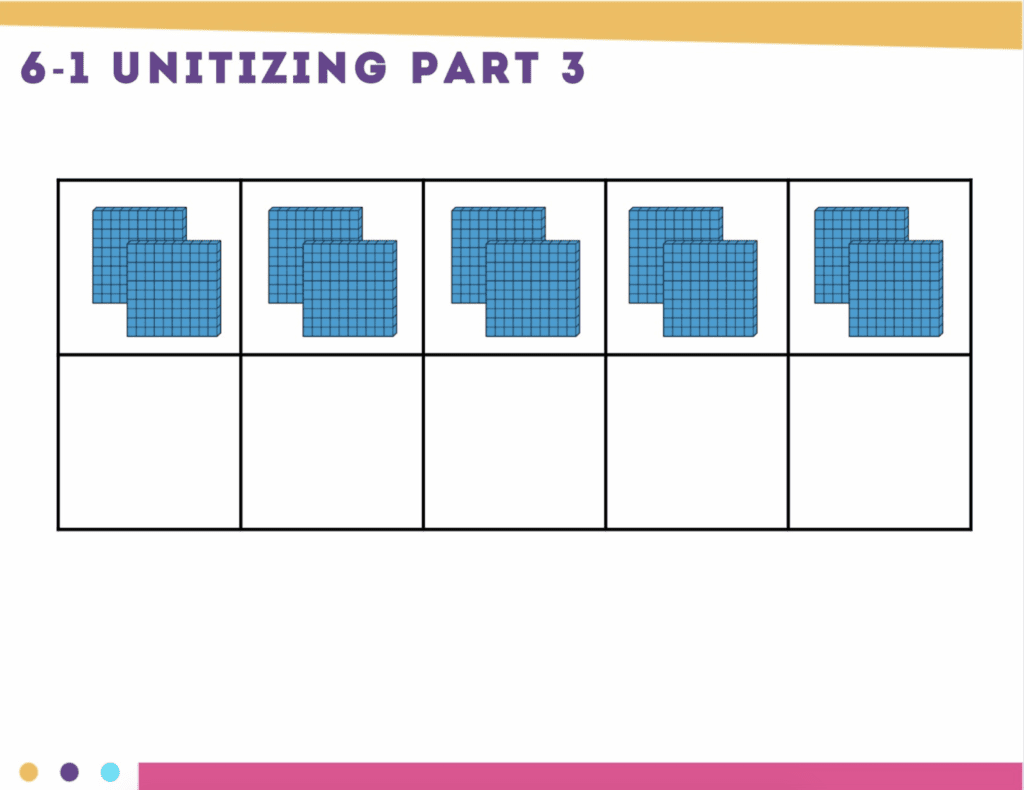
Unitizing is the counting and quantity principle that refers to the understanding that you can count a large group of items by counting smaller, equal groups of items from within the large group. This is a HUGE shift in thinking for students, and is often not naturally developed. Not surprisingly, unitizing is area of struggle for students as old as high school that often goes undetected.
However, its importance cannot be overstated. This is the foundation of our entire place value system. This is also what helps transition students from additive thinking to multiplicative thinking, which is an essential transition.
When completing a Quick Image activity, show the class an image for a few seconds and have students try to determine the quantity shown. After showing the image, I have students raise their hand to share the quantity, and I record their responses on our dry erase board. Once students share their quantities, show the image again for verification and to discuss the strategies for identifying the quantity.
Ten frames are great for these activities.
You can also incorporate base-ten blocks and other materials such as dice or dominoes. It helps me to see this number sense routine in action, so I have a short video that gives you can idea of what it would look like presented to students.
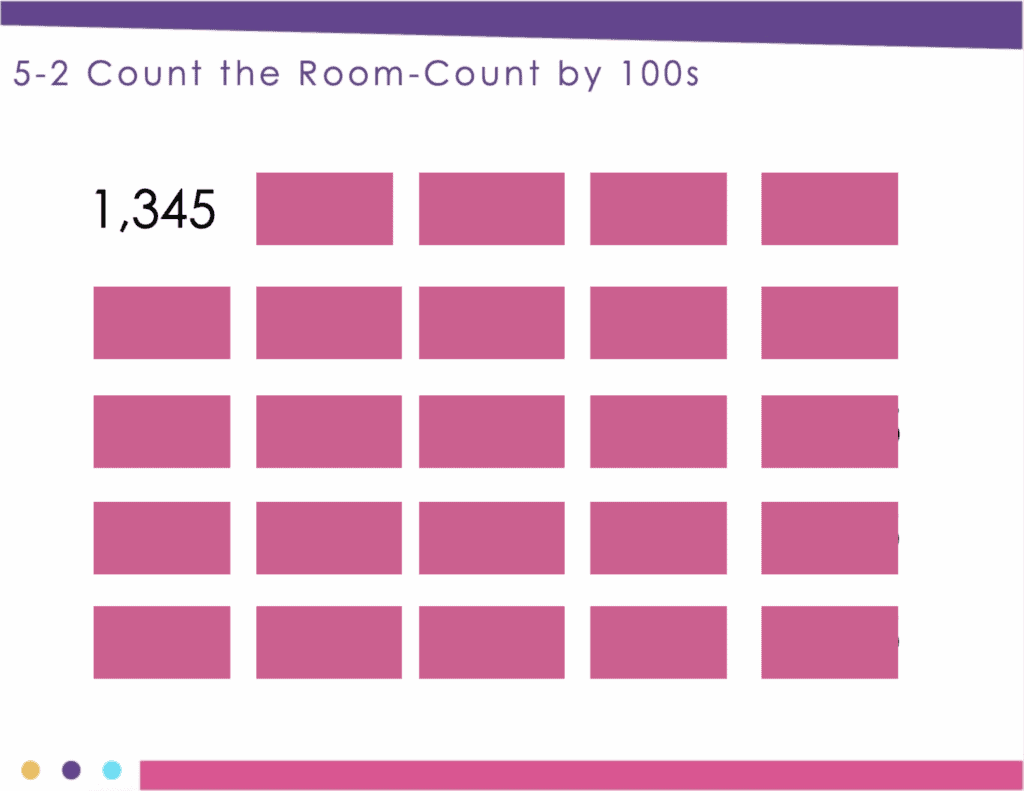
Counting
Another number sense routine are counting activities, which aren’t just for young students. Counting helps students recognize the relationship among numbers and allow students to become more proficient with math concepts. Students need repeated practice with counting to become fluent with counting sequences and to develop their number sense. One of my favorite ways to teach this is through a count around the room activity. Each person says a number as students count one-by-one around the room. To teach the procedure for this activity, start with simple numbers and sequences, so you can focus on expectations and procedures. This does work best with students sitting in a circle, but as long as students know the order in which they are counting any seating arrangement will work.
After students are familiar with the routine, begin asking questions such as, “If we are counting by fives what number will Ashleigh say? How do you know?” You may want to record the sequence of numbers as students orally count around the room.
As the year progresses, students can work with larger numbers and more challenging tasks.
There are so many options for this activity, and it’s perfect for fractions. Here’s another video for a more interactive overview for this number sense routine.
Measurement Word Problems
We all know what a challenge word problems can be for students, which is why I didn’t want to exclude them from these number sense routines or warm-ups. This is definitely not the only word problem instruction or practice that my students receive. I teach through word problems as often as possible, and I explicitly teach different parts of word problems. You can read about that here.
During our warm-ups, I incorporate measurement conversion word problems. That way, if I don’t have time to squeeze in measurement conversions before testing, my students will have experience a years worth of practice already. I start the year with somewhat simple word problems and progressively increase the level of difficulty as the year goes on.
We only complete one of these word problems during our warm-up. I don’t want to rush through the explanation in order to squeeze as much as possible in. Instead, I slow down and have students focus on sharing what information they need in order to solve the problem.
If you ever feel like any of these are too difficult, you can certainly edit the numbers in the PowerPoint file.
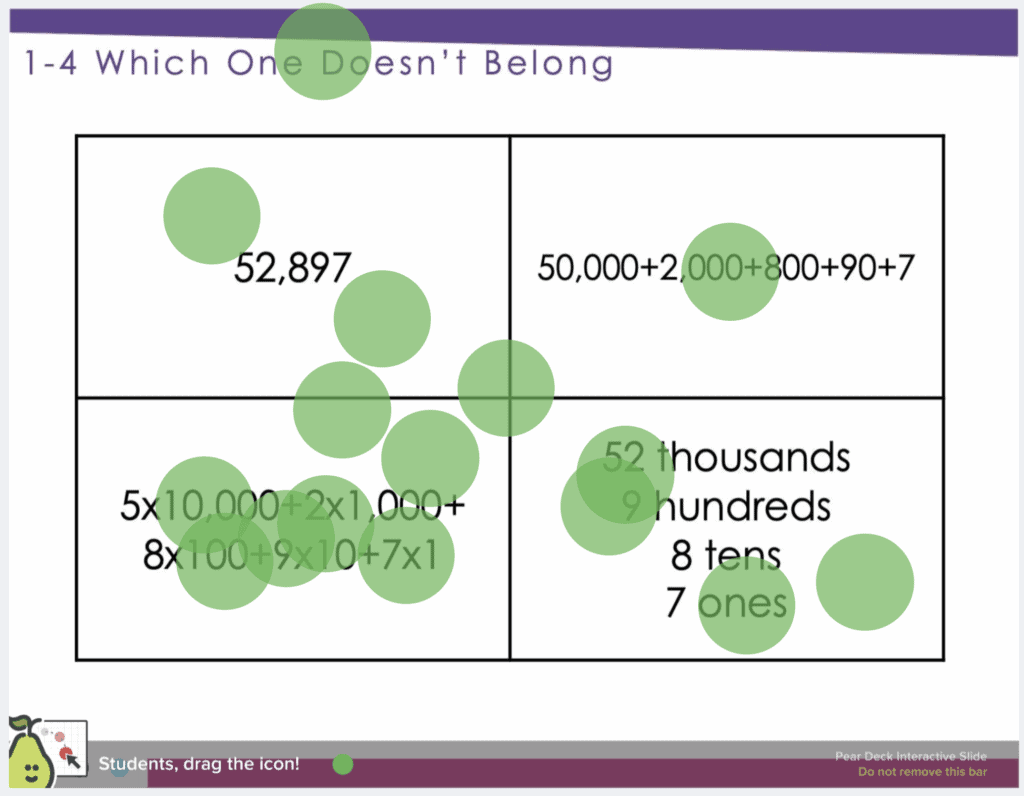
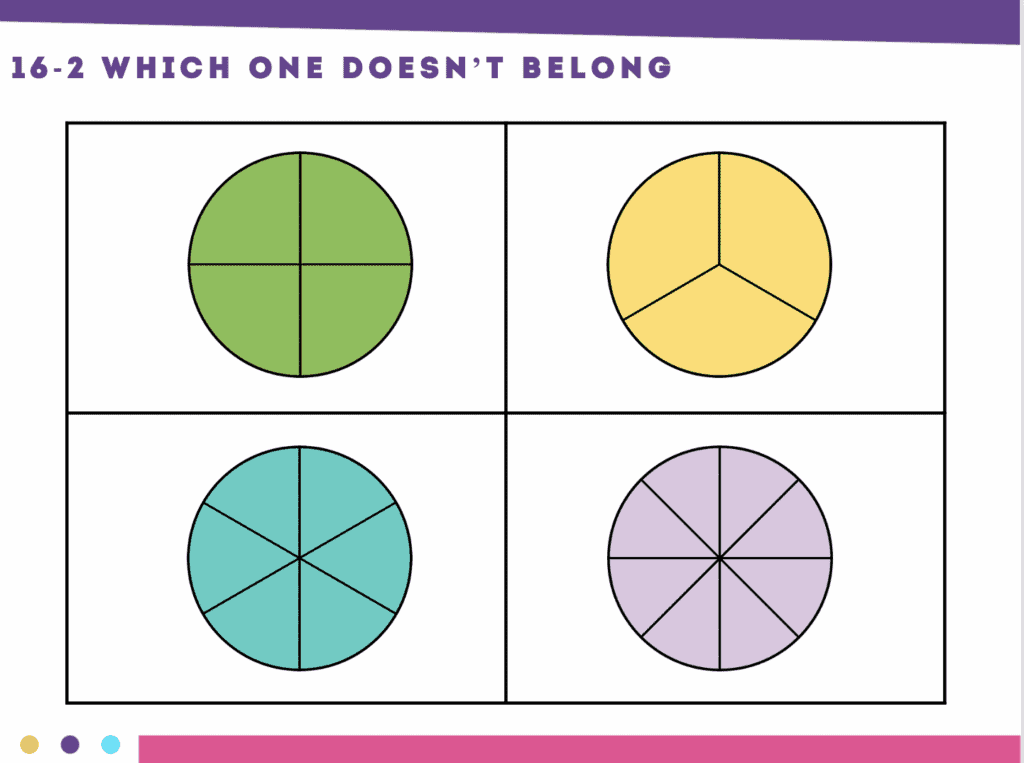
Which One Doesn’t Belong – Number Sense Routines
Students need experiences comparing groups of items by looking at similarities and differences. Christopher Danielson wrote the book Which One Doesn’t Belong and has further developed the idea on his blog. In this number sense routine students are asked to look at four images or numbers and determine which one doesn’t belong. Of course, students must also share their reasoning. Students love this routine because there are no wrong answers, as long as the student can justify his/her reasoning. The focus isn’t on the answer, as much as on the student being able to communicate his/her justification of their selection.
This is even more fun when combined with Peardeck. This lets you (and students) see what was chosen.
This is especially great for helping students develop fraction sense.
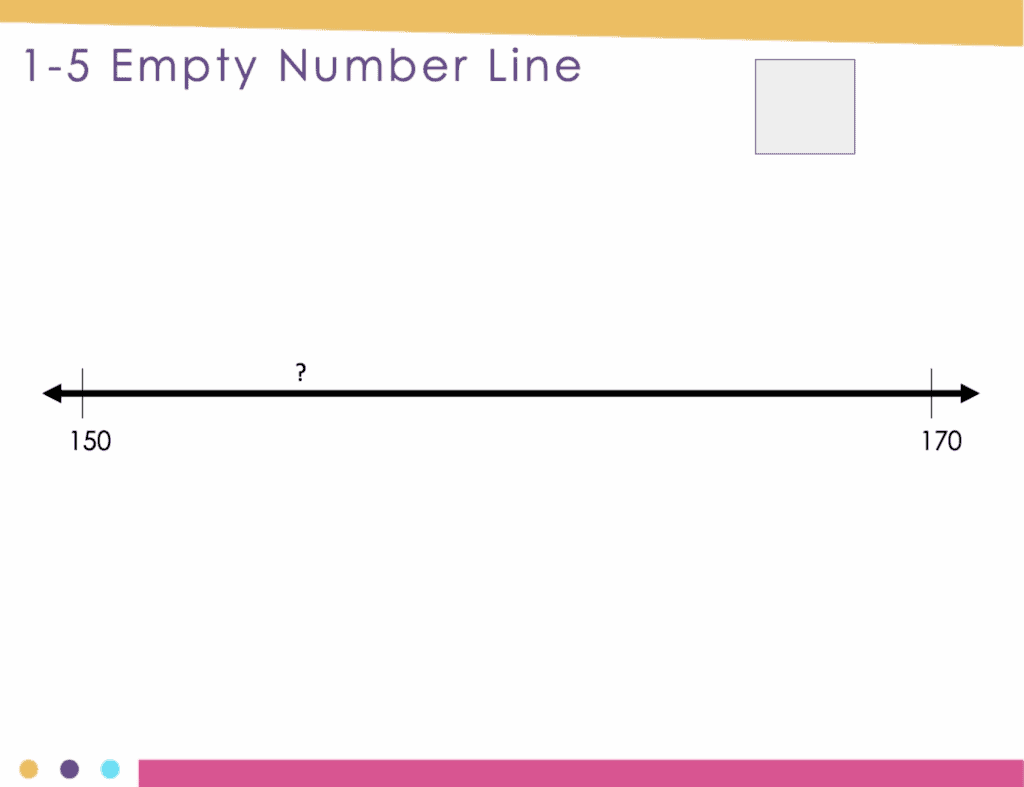
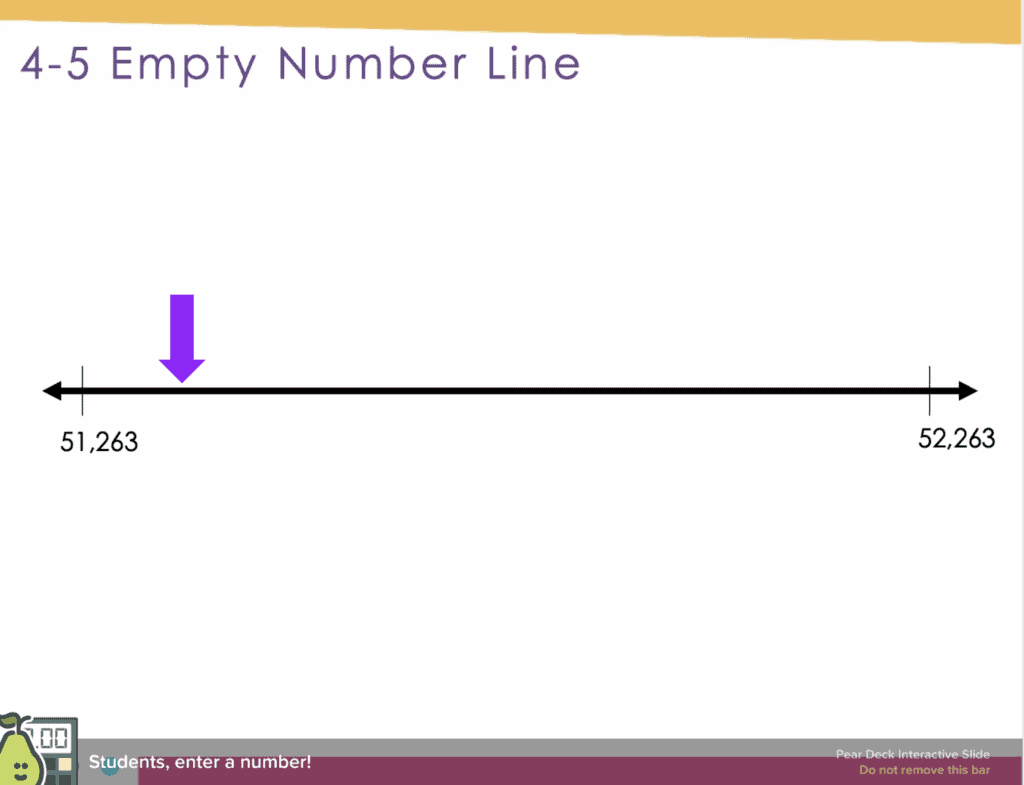
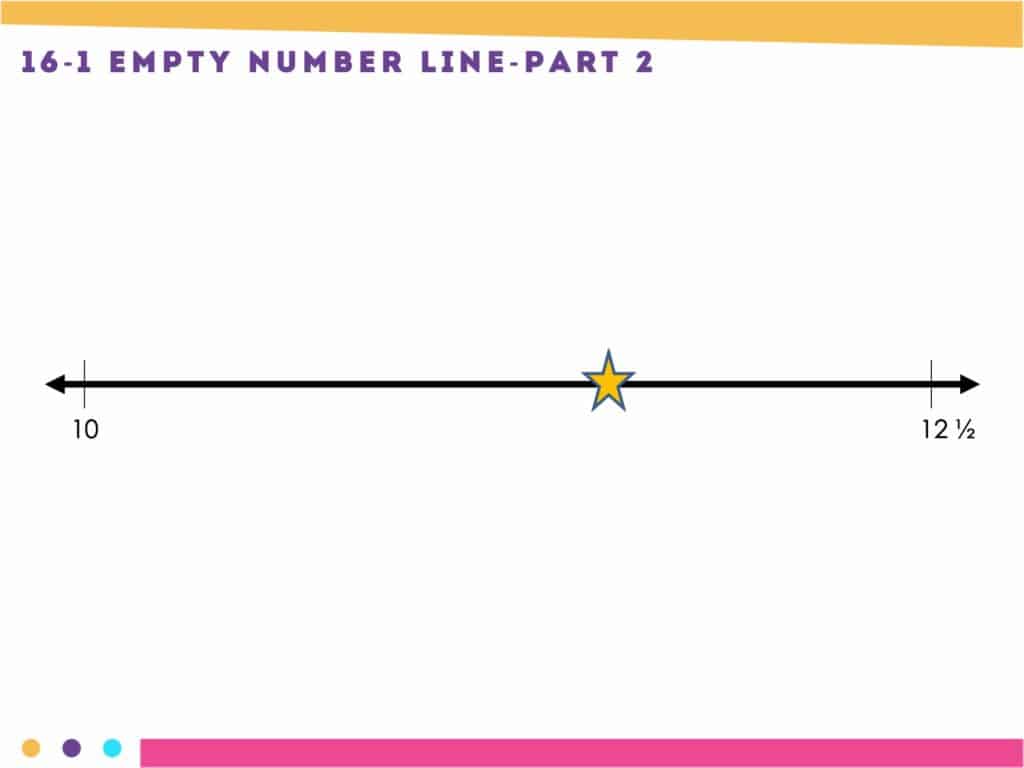
Empty Number Line
Number lines are great for your number sense routines. An empty number line is a line that is presented without markers or numbers. It acts as a visual representation for recording and sharing students’ thinking strategies, as well as providing a stage for students to think about number. The model helps students develop relations between numbers and visualize operations.
In this activity, choose a mystery number, but do not tell students the number. Show students a number line with two numbers that are at the endpoints and place a question mark on the mystery number’s location on the number line. Then, have students try to guess the mystery number. After each guess, record the number they guessed where it lies on the number line.
As with the other activities, the progressively gets more challenging as the year progresses. Plus, you can absolutely change the numbers to make the activity work with your students.
This is also particularly useful when teaching fractions and decimals. The activity provides students with the opportunity to think about the size and relative location of numbers.
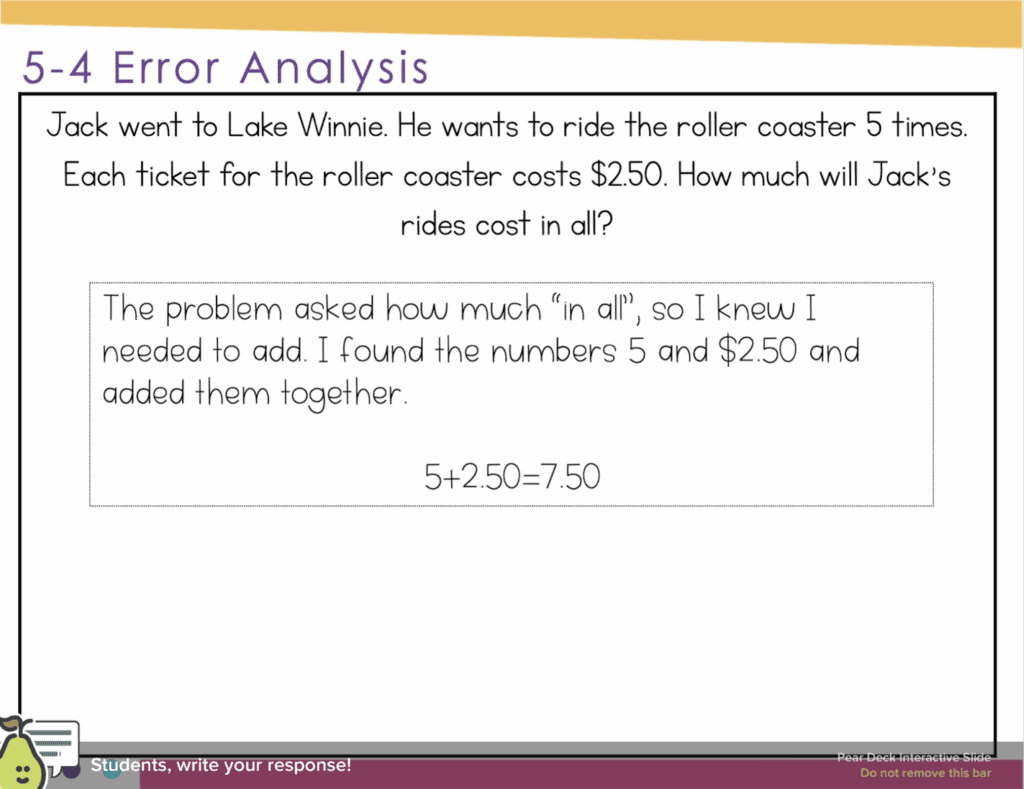
Number Sense Routines – Error Analysis
I sporadically included error analysis problems into our weekly number sense routine. In the error analysis problems, I included common errors in modeling solutions in work problems.
These are unique because the errors aren’t in the computation. The errors are in the representation of the problem. For example, in the problem below 32 divided by 8 does equal 4. However, the model does not represent the equation.
Parts and Wholes
Parts and wholes are another part of our number sense routines. This is the basis to compose and decompose numbers. One great way to teach parts and wholes is through a target number activity. The purpose of the activity is to help students think about numbers in flexible ways by having them think about how the number can be represented, composed, and decomposed. In this activity, give students a number such as 100 and have students think of all the ways they can make 100. As students develop an understanding of the routine, add constraints such as using three addends or only with multiplication and division.
As students become more proficient, they may decompose numbers into expanded notation or unit fractions. Doing these activities may allow you to see incorrect generalizations that can be addressed and retaught correctly. For example, many students try to use the commutative property of addition with subtraction. This will allow you to see what math concepts need extra time and what skills to address with students.
This is an activity where you do not need any special resources or materials. I ask the question on my whiteboard, and my students write on their personal white boards or a sheet of notebook paper. As we discuss the problem, I do have some students write their responses on the whiteboard.
I have created a YEAR’s worth of math warm-up activities to make this easier to implement. I love this because it’s all digital which saves me SO MUCH time! Of course, we all want to tailor our instruction to our students’ needs, so I’ve made the resource editable. You can click here for a FREE week!











I love this idea. There can I find this resource? The quick images make so much sense.
Thank you
I forgot to add the link! You can refresh it, and it should be there.
Do you use each of these daily or do you choose one each morning to do?
why can’t I find a link to purchase the package Number Sense Through Warm Up?
I’m not sure. There is a link at the top and the bottom of the post.