Teaching Multi-Digit Multiplication

Is it crazy that I get excited when I begin teaching multi-digit multiplication? Probably. I’ll own it. I think it’s so fun because it’s the first topic I teach that is completely new to students. Place value, rounding, addition, and subtraction are all built off of previous grades. Multi-digit multiplication is brand new. Yes, this can be a tricky topic, but there are many steps you can take to make this manageable for all students.

Before introducing multi-digit multiplication, I spend an entire week reteaching the distributive property.  Even though those lessons aren’t specifically in my standards,  they make a HUGE impact on my students’ understanding of multi-digit multiplication. Sometimes spending a little extra time upfront can save you tons of time and headache later in the year. You can visit my distributive property post here.

Teaching 4-Digit by 1-Digit Multiplication

After our week on the distributive property, I spend a week teaching 3 and 4-digit multiplication by 1-digit multiplication. I start the unit by giving students this problem. 346×7. I gave absolutely no instruction or tips on how to solve that problem.

Keep in mind that we’ve talked about struggle time and growth mindset all year. I made sure they knew that in no way did I expect a correct answer. I was simply looking for their approach and strategies they could use to solve the problem.

Out of all my students, 80% arrived at the correct answer. What impressed me even more was that only a handful of students used repeated addition. The vast majority of students used some form of the distributive property and/or partial product. Their understanding of multiplication had transferred!! The format of their work was all over the place, but that’s just a technicality. The main thing was that they understood what they were doing and the meaning of the numbers.

Area Model

I teach 3 strategies for multi-digit multiplication. While I can certainly think of more, I don’t know that’s it’s necessary to teach every possible strategy. When we teach too much too soon, students are overwhelmed and don’t learn anything well. I also make sure students have a firm grasp on one strategy before introducing a new strategy. I begin with an area model, because it is the most conceptual. Not surprisingly, I did not have a single student create an area model when they solved the problem above. I’ve found that students often do not connect arrays with area models. To help students make that connection, I use the printable below to transition students from arrays to area models. You can see that in each rectangle, the grid lines are fainter and fainter, until they are no longer visible. This helps students to SEE how area models work.

Since I teach students the relationship between arrays and area models, I encourage students to make their area models as proportional as they can. Ideally, I shouldn’t see rectangles divided into perfectly equal sections. This strategy allowed students to visualize how the distributive property worked, and since they had a solid background with the distributive property, all but two or three students fully understood area models for 3 and 4-digit numbers in a day.

The following day, while the majority of students worked in math centers, I worked with my students who needed additional scaffolding. By far, the number one problem was multiplying by multiples of thousand, hundred, and ten, so I created this printable for those students. It allows them to SEE the associative property at work while multiplying by those multiples. I certainly realize it would be much easier for me to tell students to count the zeroes, but I try incredibly hard to help students make sense of the math.

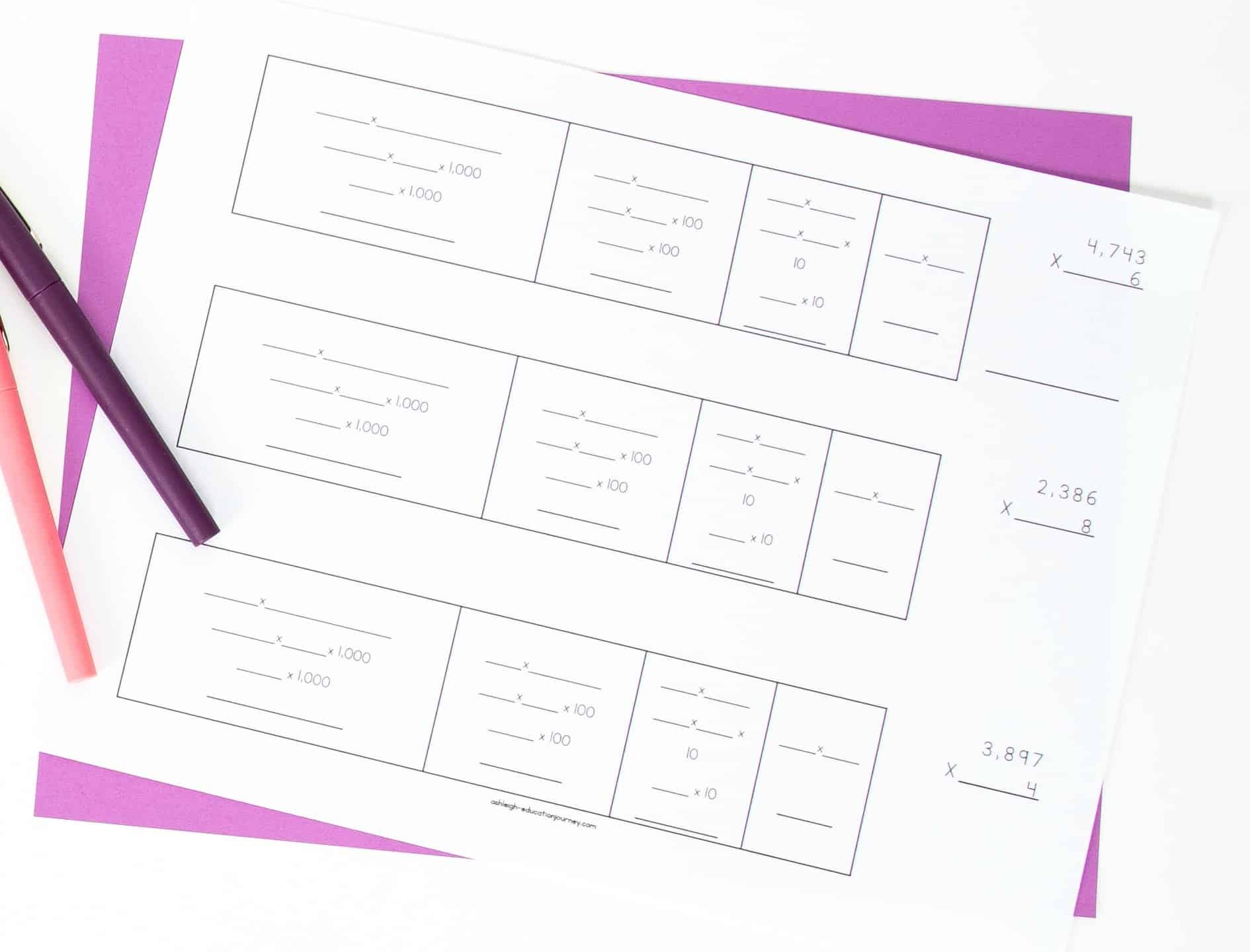
You can see what a finished section would look like. Yes, it includes A LOT of steps, but many of our students who need additional scaffolding need to SEE these steps. Eventually, they will no longer need this extreme approach, and this is so helpful in getting students to that point.

Partial Product

The following day, I introduced partial product. This is the strategy that was most natural to my students, so the vast majority quickly grasped this method. I allowed those students to work on a problem solving task involving 4-digit by 1-digit multiplication, while I met in a small group with my students who needed extra help. The following day, I continued meeting with those students, while my other students worked in math centers.

I provided these students with a step-by-step approach to partial product. This was a tremendous help, and I heard many students say, “Oh, now I get it!” A few of my students had difficulty with these because they do not know their multiplication facts. For the time being, I allowed them to use a multiplication chart. I will eventually take that away, but I don’t want them to continue to fall further behind because of multiplication facts.

Teaching 2-Digit by 2-Digit Multiplication

The next week I introduced 2-digit by 2-digit multiplication the same way I introduced 3 and 4-digit by 1-digit multiplication. I gave students a problem to solve and encouraged students to just try. It was so fun to see what strategies they invented.  This was definitely a bit more challenging for students, but their minds were activated and they were ready to learn.

Area Model

I always start with the area model, because it is definitely the best way for students to SEE 2-digit by 2-digit multiplication. The colored pictures below are the answer keys for an assignment we completed together in class. Like my previous area model lesson, I faded away the grids to arrays until there were no longer any grids inside the rectangle. This helped students to see how they were extending the area models they were previously using.

The following day, I used pages similar with the ones above for addition practice with my students who needed extra help. We met in a small group while my other students were working in their math centers.

Partial Product

I then introduced partial product for 2-digit by 2-digit multiplication. Since students had a good understanding of place value and had developed multiplicative number sense, there were quickly able to make the connection between the two models. I did have a few students who were a little confused, so I made this printable for extra scaffolding. Once again, it allowed students to see the steps and the process. I normally don’t teach math as steps and/or a process, but I realize that some students will need this systematic approach for multi-digit multiplication.

Freebies

Here’s the awesome news! Every single worksheet above, is available to you for FREE! You can access everything today with the form below.

After teaching the concept, students then move toward more abstract methods to solve multi-digit multiplication problems. I typically begin by having students use dry erase boards during our mini lesson. This makes the practice so much more engaging for students, and it saves on paper! If I see that students have the concept mastered, they complete a problem based task during our work time. If I see that a student needs extra help, I work with those students in a small group.

Occasionally, I do have students practice on paper. I like to have something to send home so their parents can see the strategies in use. Plus, consistent practice is important. All of the practice sheets below are from my 4th Grade Multiplication Unit.

I save the algorithm for last, because it’s the most abstract way to solve multiplication problems. Once my students are comfortable with each way to solve multiplication problems, I allow them to use whichever method they prefer. Just out of curiosity, I surveyed both of my math classes on their favorite strategy, and the algorithm won by far. However, every student who struggles a bit with math chose either the area model or distributive property

I incorporate problem solving throughout the multiplication unit.

You can see my Multiplication Unit here.

At the risk of being a bit cheesy, I also wanted to share a little video I made on 2-digit by 1-digit multiplication.