Dividing with area models and partial quotient is a major part of fourth grade standards. Confession: when I first moved to fourth grade, I had no clue how to divide with an area model or partial quotient! After teaching it to myself, I hated it! Dividing with area models and partial quotient didn’t click for me until I was actually teaching my class. All of a sudden, the pieces fell into place, and it all made sense. Hopefully, this post will save you the headaches I experienced learning this important concept.
One of the reasons dividing with area models and partial quotient was confusing for me is that I had not learned multi-digit multiplication or division conceptually. As a student, I only understood procedures. You can read more about the value of teaching both concepts and procedures here. In this post, I’ll keep the focus on multi-digit division.
For students to fully understand multi-digit division, they have to understand the concept of multiplication. If you want to see how I teach multi-digit multiplication, be sure to check out this blog post. It all ties together.
When teaching dividing with area models and partial quotient, we don’t want the strategies to be a series of steps for students to follow without any real meaning. We want students to grasp the how and why of what they are doing and to become flexible in their thinking. All of the printables shown in this post are from my division unit. Even without the unit, you should be able to get a lot of good ideas for teaching dividing with area models and partial quotient.
First Review
Before introducing multi-digit division, backtrack a bit and spend a little time on the concept of division. It’s essential that students understand that division is repeated subtraction of equal groups. If students can firmly grasp that idea, dividing of larger numbers is so much easier. Teach a few hands-on division lessons that are a review of students’ third grade standards. I’ve found that this review is critical. Otherwise, students tend to look at me with blank stares as we discuss division vocabulary and concepts.
Teach Division Concepts
Before teaching dividing with area models and partial quotient help students connect place value and division. Students use base-ten blocks and pictures to model long division problems. This activity helped solidify students’ understanding of the concept of long division, and the base ten blocks helped make the concept more concrete.
You can also show students how to use multiplication to solve long division problems. While this is fairly simple with problems such as 36 divided by four, it can be more challenging when the dividend is a larger number.
In this activity, students broke the division problem into partial products and found the missing number in the partial products. They were absolutely blown away when they saw this strategy for solving division problems! It is also great reinforcement for the distributive property. I began with heavily scaffolded problems and gave students more and more responsibility as they progressed through the assignment.
Students can also solve division problems with division, rather than multiplication. This was a natural progression for students, and it actually made sense to them. They recognize the connection between using multiplication and division, and the grouping strategy began to have more meaning to students.
Dividing With Area Models
While I strongly prefer using partial quotient for multi-digit division, dividing with area models help students build essential conceptual understanding. I begin this lesson by drawing the area model and having students label the parts of the area model and the division and multiplication number sentence represented by the area model. This was another “ah-ha” moment for students, because until this lesson, they did not understand why they were using the area model to divide.
While this lesson was valuable for students, this is something that students need multiple experiences with, so I continue to teach area models until I feel like most students have a solid grasp on the concept. I heavily emphasize correct vocabulary, how arrays are used in division, and why we might prefer an area model to an array.
In my class this year, I could tell the my students were getting a little tired of arrays and area models. I tried to bring in a little humor with silly titles for their practice pages. Let me tell you, it worked WAY better than I expected.
It quickly turned into a thing, and my students started to expect a silly title, and for as hard as they were working, I was happy to oblige. While I do spend a lot of time on one concept that is just a small portion of division, the understanding that students develop through those lessons is so beneficial in the long run.
It typically take about a solid week of instruction for students to completely grasp the concept of dividing with area models. When the pieces finally click together, students understanding the meaning of what they’re doing, which makes the remainder of the unit so much easier.
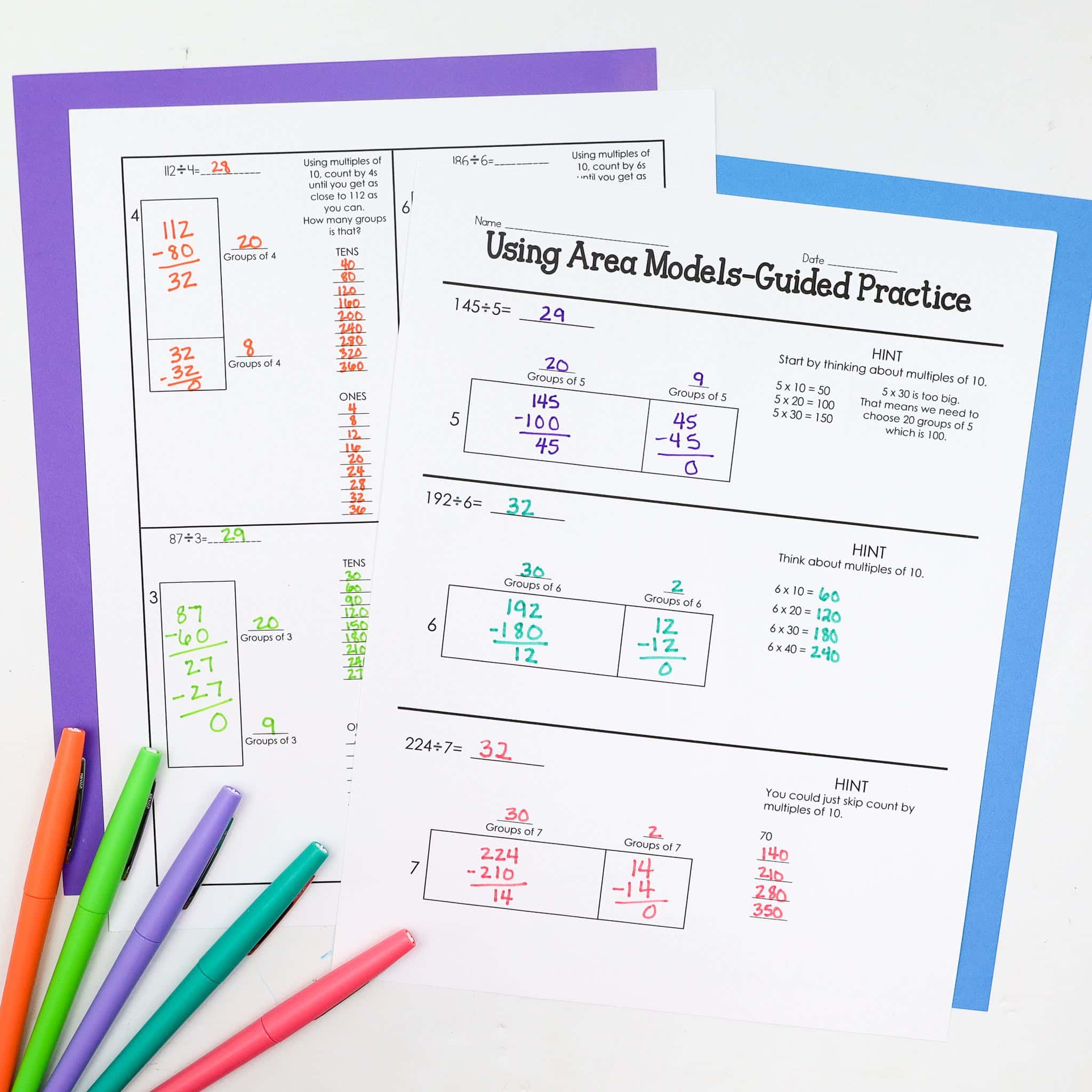
Dividing With Partial Quotient
After dividing with area models, I progress into partial quotient. We begin with more area models, and I slowly fade away two of the lines in the rectangle. I do this to allow students to see the connection between area models and partial quotient. With all the experience with area models, students are blown away with the simplicity of partial quotient.
It’s also helpful for students to see how they can use different strategies or different numbers to arrive at the same result. In one lesson, students divide the same numbers four different ways, so they can see how they can take away different groups of numbers from the dividend to arrive at the same quotient. I also like to have students begin writing about division, because I try to incorporate a lot of writing into my math instruction. In this lesson, students explain which method was most efficient for them and why.
No matter how hard you work on multiplication facts, you will more than likely have a handful who have trouble with division because of multiplication facts. While I want students know their multiplication facts, I don’t want students to completely miss the division lessons because of multiplication facts. One of my favorite strategies is to teach students how to skip count by the divisor to help solve the division problem. I provide a couple pages where I’ve skip counted for students, so they can see how much easier it is to divide with that information. After the initial introduction to that strategy, I require students to show their skip counting on an as-needed basis.
Dividing With Area Models – Problem Solving
The remainder of my division lessons are centered around problem solving. During the problem solving lessons, I meet with students who need more foundational lessons in a small group. On some days, we may complete the problem solving lesson together. On other days, they may skip the problems solving lesson, while we work on something a little more basic.
It’s essential that students see the value and purpose in learning to divide. I always explain that in the real world, no one grows up to complete worksheets for a living. Instead, we use math to problem solve. I try to make these problem solving lessons meaningful and connected to my students’ lives.
Divisibility Rules
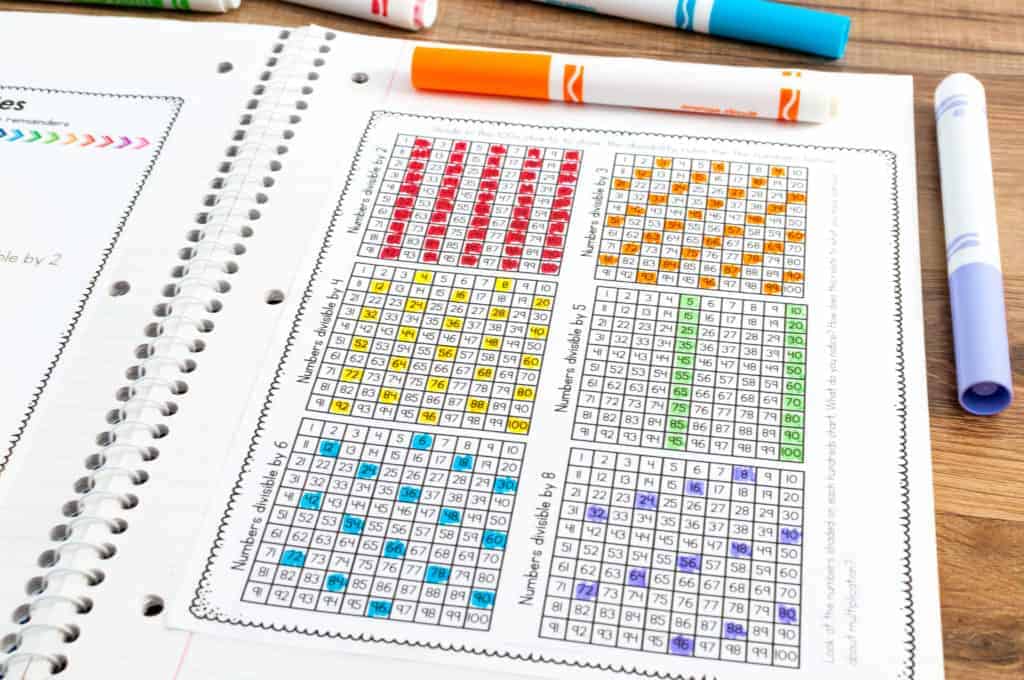
While it’s not in my standards, I do introduce the term and concept of divisibility. It’s not important for this concept to be mastered at this time, but it’s nice to allow students to begin developing an understanding. I created a divisibility rules entry for my students’ interactive math notebooks. One side lists divisibility rules for 2, 3, 4, 5, 6, 8, 9, and 10. The other side includes six hundreds charts where students shade in numbers that are divisible by particular numbers. You can download the Divisibility Rules entry here.
I hope that you were able to gain a lot of ideas from this post! Remember, you can find all of the lessons and printables here. Also, don’t miss out on my Division Escape Room blog post. That shows how I culminate our division unit.
