
There is definitely an art and science to teaching elementary math. Despite what you may read or hear, there is also no one right way to teach math. Far too often experts support an all-or-nothing approach. However, those of us in the classroom realize that our students have varied needs, and we have to tailor our instruction to meet those needs. In this post, I’ve shared best practices and foundations for teaching math. These are all strategies I have successfully used for years in my own upper elementary classroom.
Core Math Instruction
Before diving in, I want to specify that these practices are for your core math instruction. Core curriculum is the instruction provided to all students in the general education classroom. This math instruction combines an understanding of how students learn, how to teach through problem solving, and how to plan for and assess learning. You may have some students who do not respond successfully to your core math instruction, but this should always be a small percentage of your students.
Doing Math
Math is more than completing sets of exercises or mimicking processes the teacher explains. When students are doing math they generate strategies for solving problems, apply those approaches, see if those approaches lead to solutions, and check to see if their answers make sense. If students’ minds are not actively engaged, no effective learning occurs.
I like to think that my students are doing math, but I often find myself taking cover. Eventually I’m the one doing the math, and my students are observers. One strategy to determine who is doing the math is to ask students to describe math. In a teacher centered classroom students often describe math as: work, getting answers, plussing, etc. In a student centered classroom students may use words such as: solve, discover, represent, or justify. When students do math they shift from knowing math to understanding math.
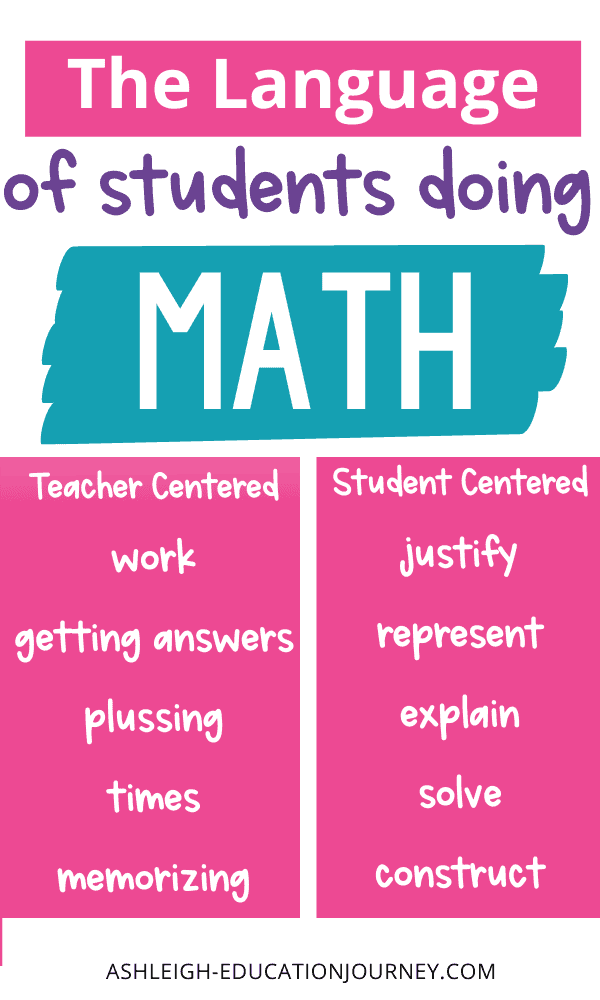
Understanding Math
Understanding math is rarely all or nothing. In low levels of understanding ideas are isolated, easily forgotten, and unlikely to be used for constructing new ideas. High levels of understanding associate ideas in a meaningful network of concepts and procedures. High levels of understanding allow students to more easily learn new concepts, because they can connect new ideas with previously learned concepts.
There are two primary types of understanding: conceptual and procedural. Conceptual understanding is knowledge about the relationships or foundation ideas of a topic. Procedural understanding is knowledge of the rules and steps used in carrying out processes and the symbolism used to represent math. Both types of understanding are needed. Conceptual understanding is an important component of procedural proficiency, because without conceptual understanding common error patterns occur in students’ procedural work. Since students who are skillful with a procedure are reluctant to attach meaning after the procedure is mastered, procedures should be taught after the concept has been developed.
Multiple Representations
The more ways students are given to think about and test ideas, the better chance they will integrate it into a web of concepts and develop a deep understanding. When students strengthen their ability to move between representations, their understanding and retention also improves.
A model for a math concept refers to any object, picture, or drawing that represents a concept. Manipulatives are objects that students can use to illustrate and discover concepts. We have to be careful to avoid using models and manipulatives inefficiently. One common mistakes is to show students exactly how to use the manipulatives. Students mimic our directions and may look as if they understand. However, the could be mindlessly following what they see, which does not promote understanding. When we do this, students may begin to use models as answer-getting tools, rather than resources to explore a concept. On the other hand, leaving students with insufficient guidance results in nonproductive investigations. We should introduce models by showing students how they can represent the ideas for which they are intended.

Teaching Elementary Math Through Problems
The most important principle for teaching math is to allow math to be problematic for students. Students should solve problems, not only to apply math, but to learn math. A problem-based task is an activity where students have no prescribed or memorized rules or methods, and there is often not a correct solution method. Teaching through problems solving helps to focus students’ attention on ideas and sense making. It also helps to provide a context to help students build meaning for the concept grounded in the task.
There are three primary features or requirements for teaching through problems:
- The problem must begin where students are in their zone of proximal development.
- The problematic aspect of the task must be due to that math students should learn.
- The problem must also require justification and an explanation for students’ answers and methods used to solve the problem.
In my experience the most challenging part of teaching through problem solving is finding or creating appropriate tasks. A good task will have multiple entry points. For example, if students were asked to find the area of the cover of a book, the cover of the book can be completed covered with tiles and then counted one at a time. Students may cover the book with tiles but only count the length and width. Students may only place tiles on the edges of the book, while another student may use a ruler to measure.

Three Part Lesson for Teaching Elementary Math
Most math lessons will have three parts: before, during, and after. There are many names for these parts, and more than likely what they’re called is irrelevant.

In the before stage, you want to mentally prepare students for the task. You may need to review prerequisite skills needed for the task or could begin with a simple version of the task. In this stage you also want to make sure students understand the problem or task before having them get started. Discuss what information is provided in the problem and help students clarify what the problem is asking. Since most tasks require more of students than simply the answer, students should be prepared to explain their thinking. Your expectation for how students will share or explain their work must be made clear at the outset of the lesson.
In the during stage, give students a chance to work without your guidance. Give students the opportunity to use their ideas and not simply follow directions. This is so much easier said that done and problems do arise. To avoid an excessively long post, I linked two helpful posts for this portion of your lesson. One is productive struggle and the other is on learned helplessness.
It is certainly okay to help students during this time. You just want to avoid solving the problem or taking away the need for students to reflect on the situation and to develop solution methods. Students must be told conventions such as math symbols and vocabulary.
Students will almost always look to you for approval of their results or ideas. Even though it’s hard, avoid being the source of right and wrong. When asked if a result is correct, ask, “How can you decide?” or “How can you check that?”.
The after stage can also take many different approaches. If there are multiple solutions to a problem list all answers and have students share the explanation for their solution. During this state you will want to summarize main ideas and address potential problems, misconceptions, or over generalizations.
Teaching Elementary Math – Next Steps
Research and data indicates that at least 80% of your students to achieve proficiency in math. With additional instruction (RTI, SST, MTSS), that percentage should increase to 90%-95%. However, the effects of Covid has skewed these numbers. Teachers are seeing a much higher percentage of students not responding to the core instruction described in this post. This is where our next steps will be!
Blog Series
This will eventually be a complete blog series for teaching students who have difficulty in math. You can find the other posts below.
Math Facts
Ways to Learn More
Ready to Use Math Units
If you’d like to see my core instruction for teaching elementary math, check out the links below:


Professional Development Course
If you’d like to dig deeper into core math instruction, be sure to check out this professional develop opportunity!

Teaching Elementary Math Blog Posts
I didn’t share content specific posts. There are just too many to choose from! However, these are great general teaching elementary math posts.
How to Structure Your Math Block
Teaching Math Workshop Procedures
8 Things Teachers Say to Create Misconceptions in Math
Why I Want My Students to Have Struggle Time
Preventing and Ending Learned Helplessness
Number Sense Through Math Warm-Ups
5 Ways to Increase Engagement in Math


