Equivalent Fractions

In my Fraction Unit there is a heavy emphasis on equivalent fractions. As students develop their fraction number sense, they typically come to the realization that some same-size fractions have different names. This gives a natural transition to teaching equivalent fractions.

Before teaching the procedure of multiplying the numerator and denominator by the same number, students must develop an understanding of equivalent fractions.

Teaching the Concept of Equivalent Fractions

Students often need a little prompting to see equivalent fractions. One way to do this involves using grid paper. I added the outline of a region and designated it as one whole. Within the whole, one part of the region is lightly shaded. Students use different parts of the whole to determine multiple names for the part.

This is what the digital version of the lesson looks like. This year I ended up printing the digital version, and I really loved that format!

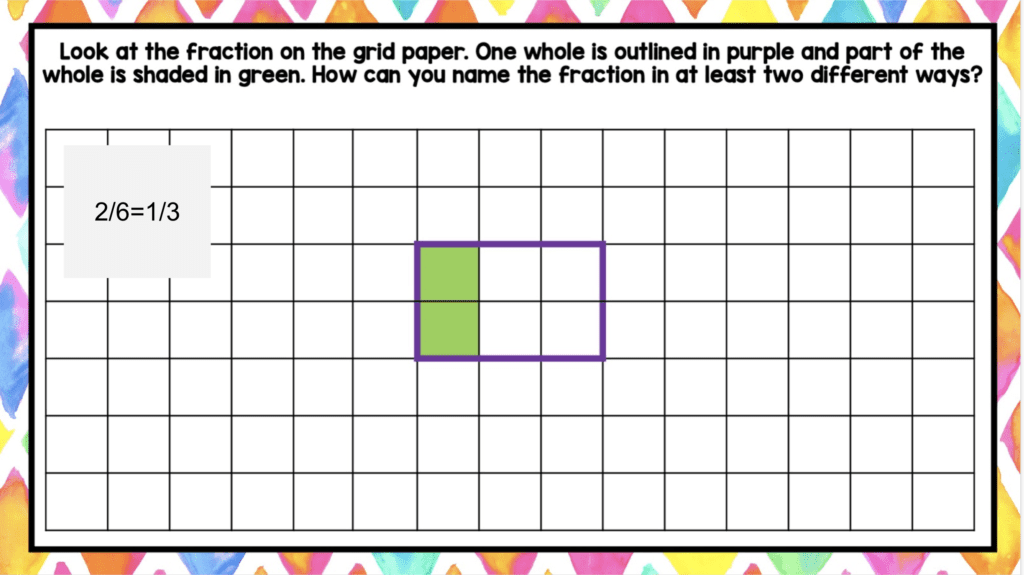
Students typically need more than one conceptual lesson before seeing the procedure on their own. That’s why in the following lesson students continue to work with grids to identify equivalent fractions.

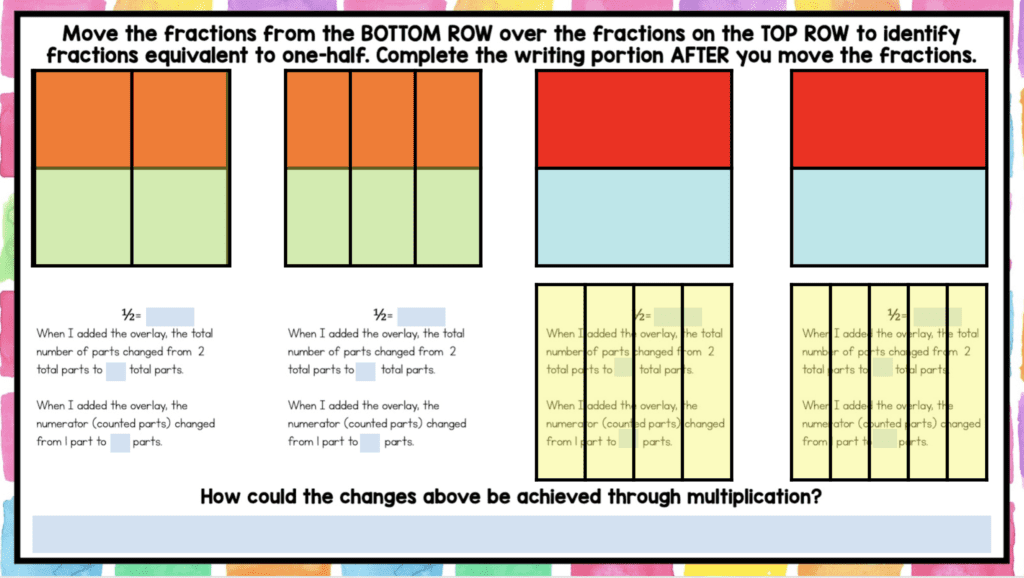
This is a lesson that all students complete digitally-even if we’re face-to-face. Students move translucent fraction pieces to generate equivalent fractions. It’s during this lesson that students begin to get it.

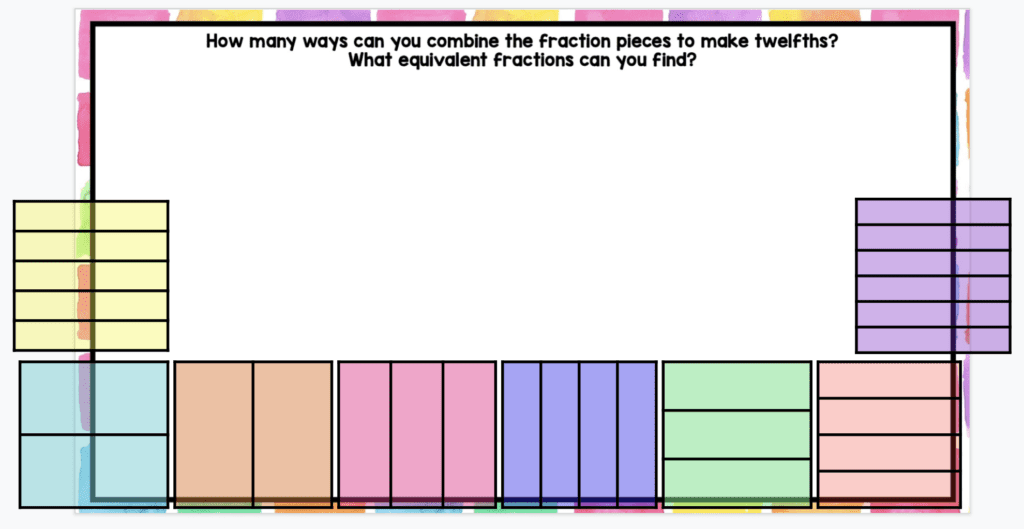
In one page of the lesson, students try to find all the ways possible to combine fraction pieces to make twelfths. This was really beneficial to some students, because it allowed them to connect multiplication and fractions.

 

Teaching the Procedure of Generating Equivalent Fractions

The following lesson begins transitioning students into discovering the rule or procedure for generating equivalent fractions. The goal is for students to see that if they multiply the numerator and denominator by the same number, they will generate an equivalent fraction. One way to teach this is through an area model approach. Students slice each square into an equal number of horizontal slices and write an equation showing the equivalent fraction.

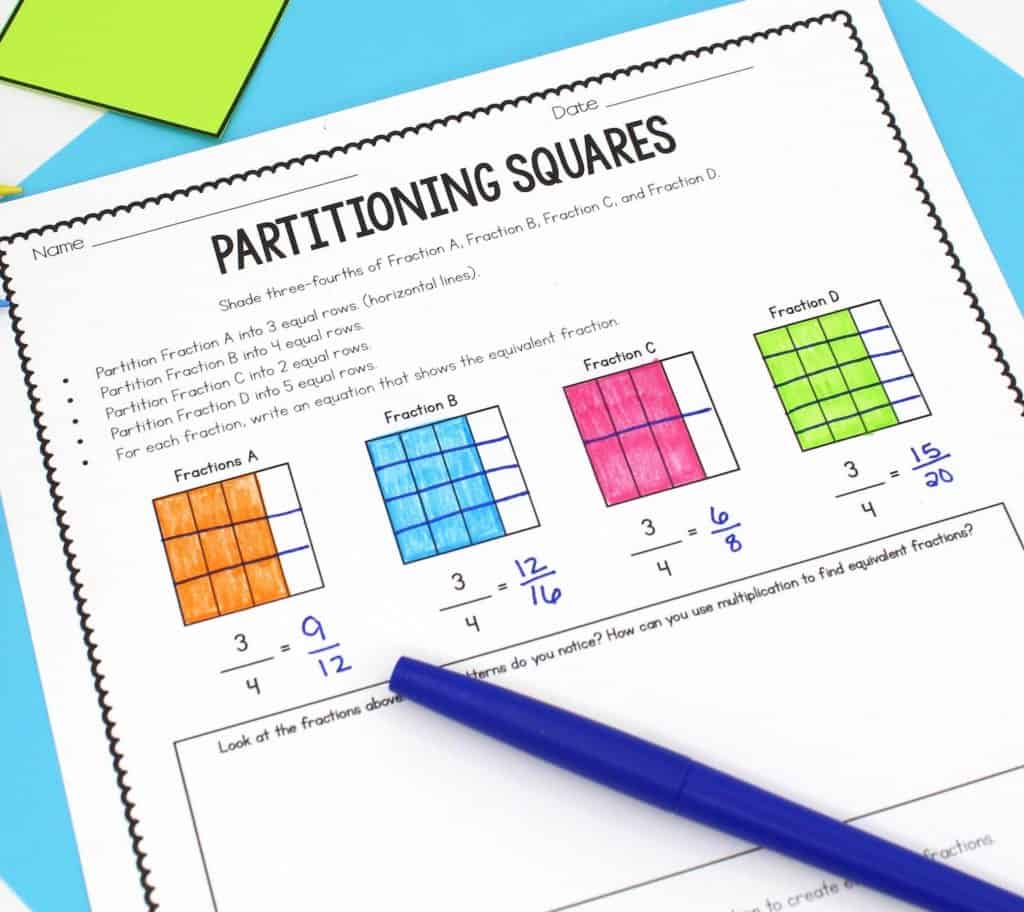
This is what the digital version of this lesson would look like. Students would drag the bar to partition the fractions.

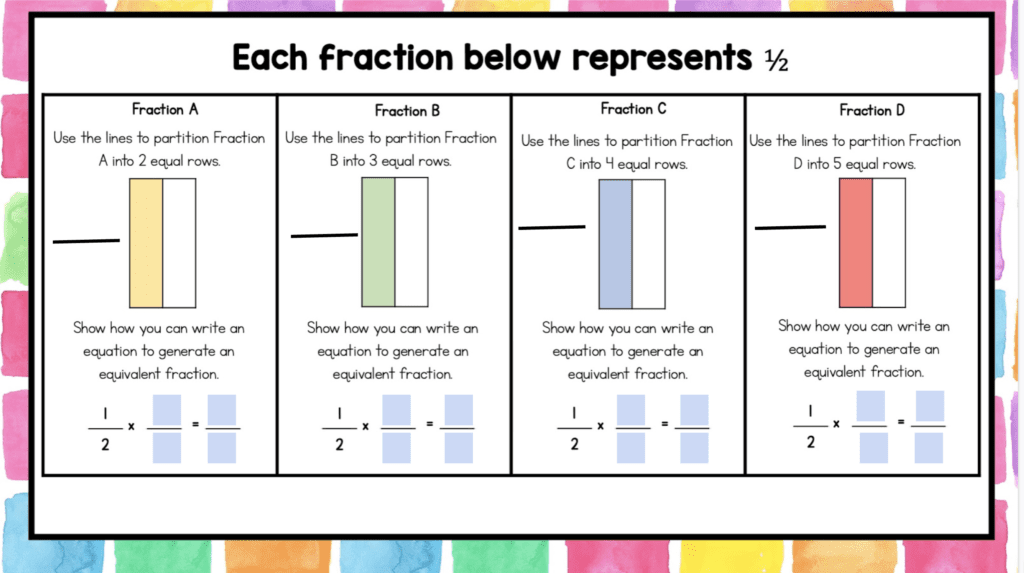
Follow the lesson with a class discussion on the rule for generating equivalent fractions. The discussion is important, because many students will only count the squares without thinking about the connection to multiplication. To support the procedure, give students an equation showing equivalent fractions, but one of the numbers is missing.

Equivalent Fractions – Problem Solving

Once students have been explicitly taught how to generate equivalent fractions, they should focus on problems solving tasks where they apply their understanding of equivalent fractions. Students love this pattern block lesson, where the size of a whole is TWO and sometimes THREE hexagons. It requires students to change the way they look at the whole, because most students identify one hexagon as a whole.

This lesson can also be completed digitally. Students will move digital fraction block pieces in the digital version.

I like to have students continue to explore equivalent fractions through literature that moves students into problem solving situations. Real literature is optimal for this, but everything I found was a bit too young for my students and focused only on the size of fractional parts, rather than fraction equivalencies. Finally, I took a chance and wrote my own “book”. You can download that book for free here.

As a math center activity, students use models to find different names for fractions. One way to teach this is to give students outlines of different fractions and have students use their fraction pieces to find as many single fraction names for the region as possible. You can download that lesson below!

You can find all of the lessons above in my 4th Grade Fraction Unit.

You can find a HUGE collection of fraction posts here!