Most curriculums and textbooks make a lot of assumptions. That’s especially true in math. For instance, in fourth grade, students jump right in to multiplying a 4-digit number by a one-digit whole number and then multiplying 2-digit numbers by 2-digit numbers. Years of experience has taught me that the majority of students are not ready to make the leap from third grade multiplication to fourth grade multi-digit multiplication. They need transitional lessons that bridge what students learned in third grade to what students will learn in fourth grade.
Students need more time and learning opportunities. Many students are not developmentally ready to fully understand concepts such as the distributive property or multiplying by multiples of ten in third grade. However, with additional instruction the following year, the missing pieces often click. These two concepts are essential for understanding multi-digit multiplication, so these transitional lessons are incredibly important. The lessons below are from my 4th Grade Multiplication Unit. If you’re looking for 3rd grade multiplication ideas, be sure to check out this blog post.
Multi-Digit Multiplication Basics: Multiples of Ten
One of the most important concepts for students is multiplying by multiples of 10, 100, and 1,000. This is extremely difficult for students who lack number sense. While it may seem obvious to us as adults, these students do not see the relationship.
Introduction
I like to introduce this concept with a digital activity, because whether I’m face-to-face or teaching virtually, manipulatives tend to get a bit out of control with this lesson.
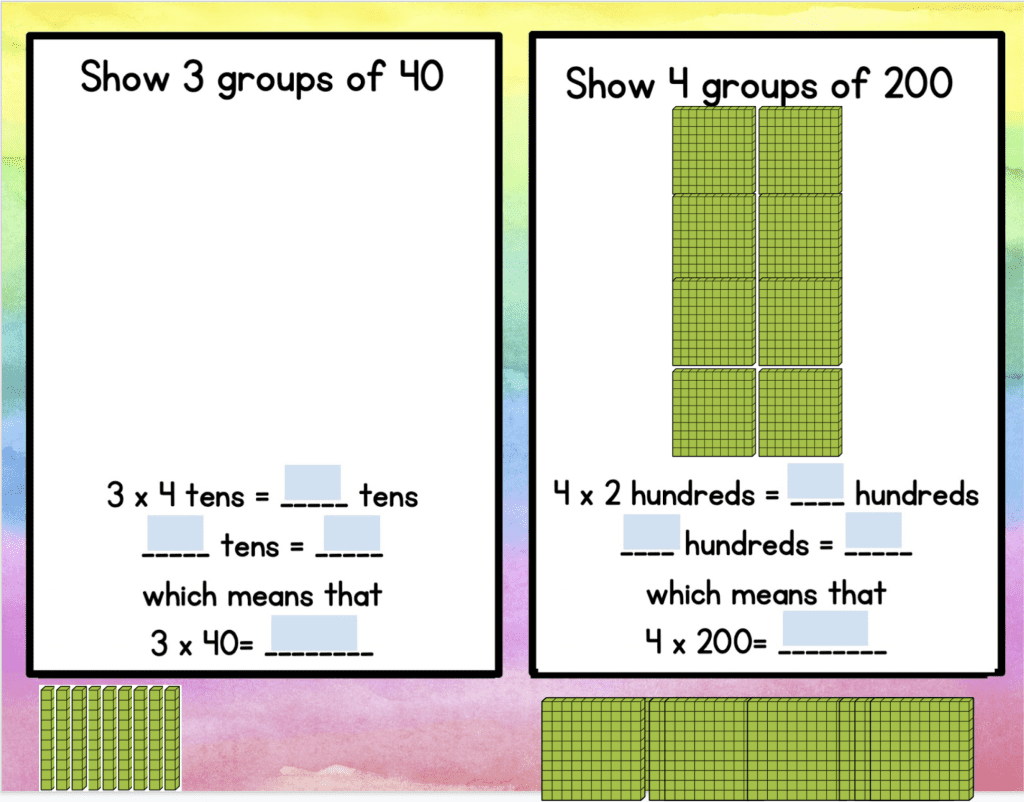
Students first use base-ten blocks to build different multiplication situations. This allows them to see how 3 groups of 40 is the same as 3 groups of 4 tens.
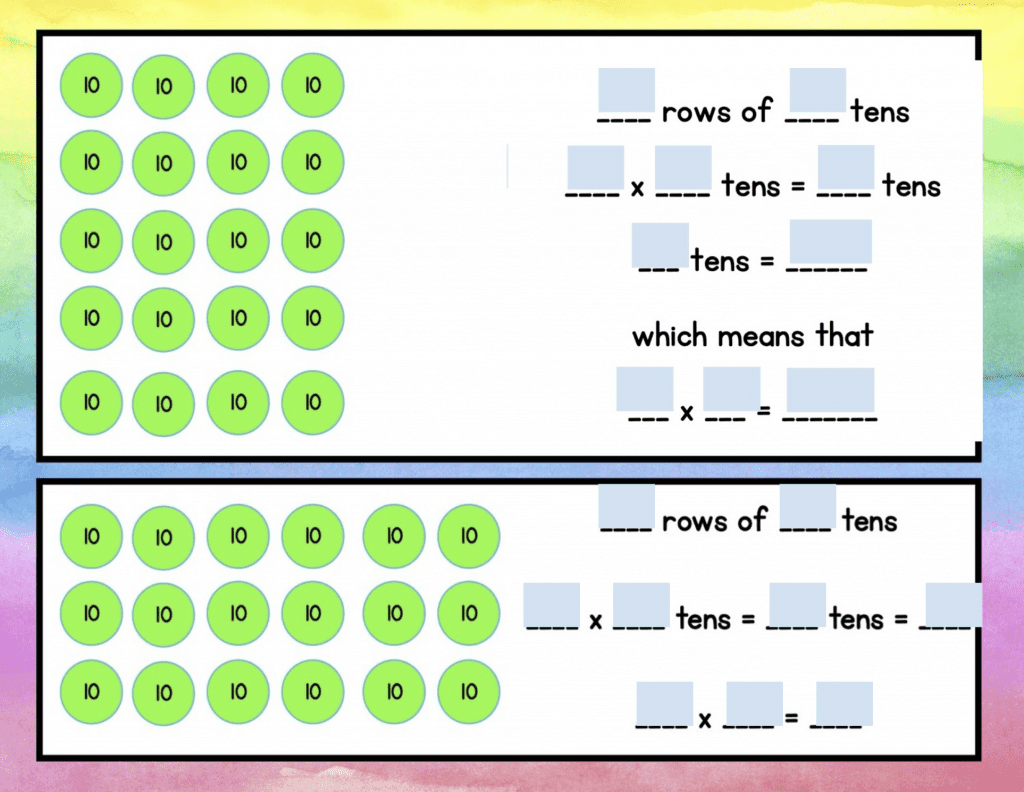
Students then use place value chips (that’s what we call them) to analyze arrays. For example, there are 6 rows of 4 ten, which represents 6 x 4 tens. By doing this, students should realize that 6×4 tens equals 24 tens.
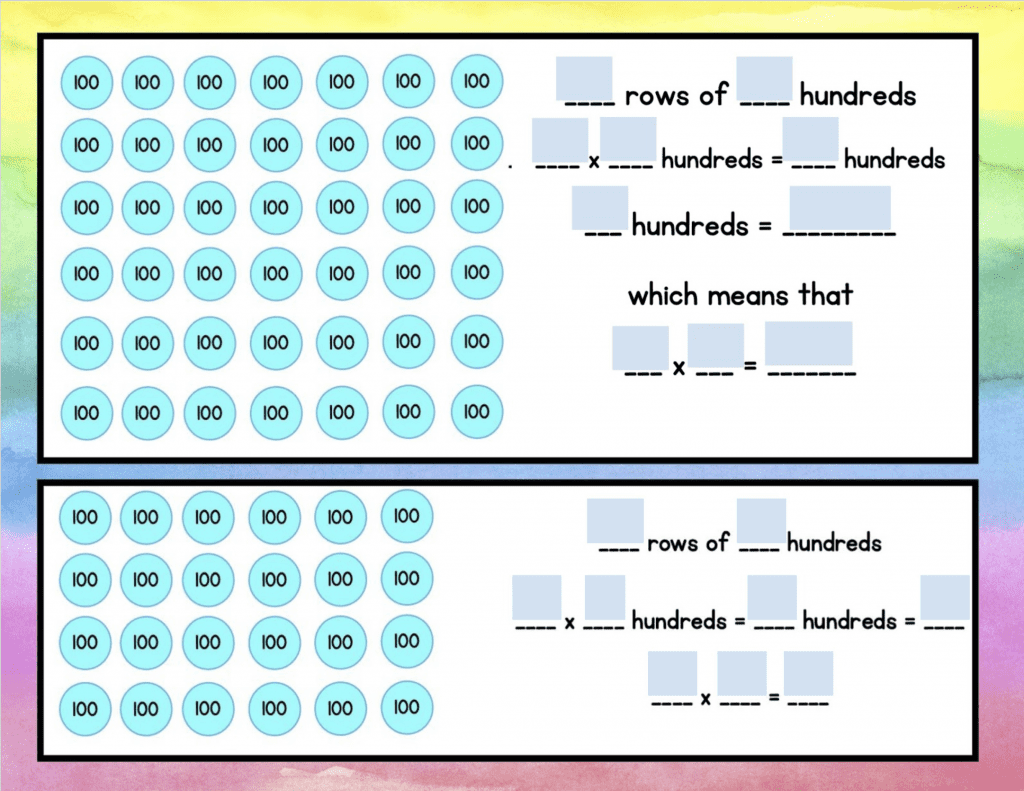
Students do the same type of task with hundreds, which helps to solidify the relationship of multiplying ones, tens, and hundreds.
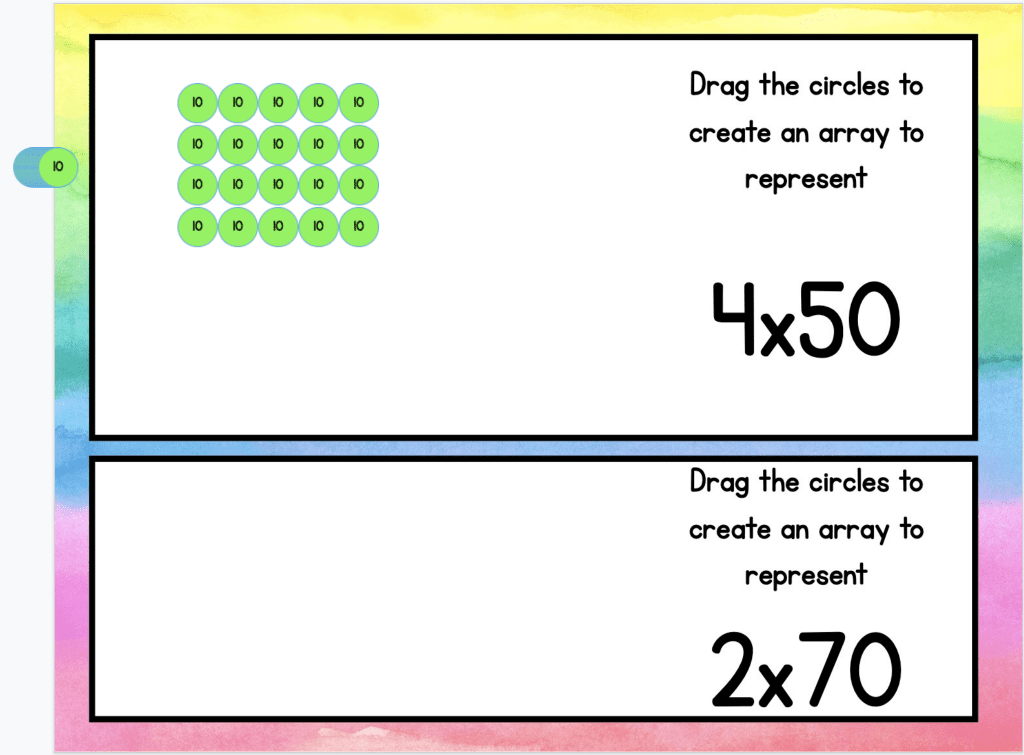
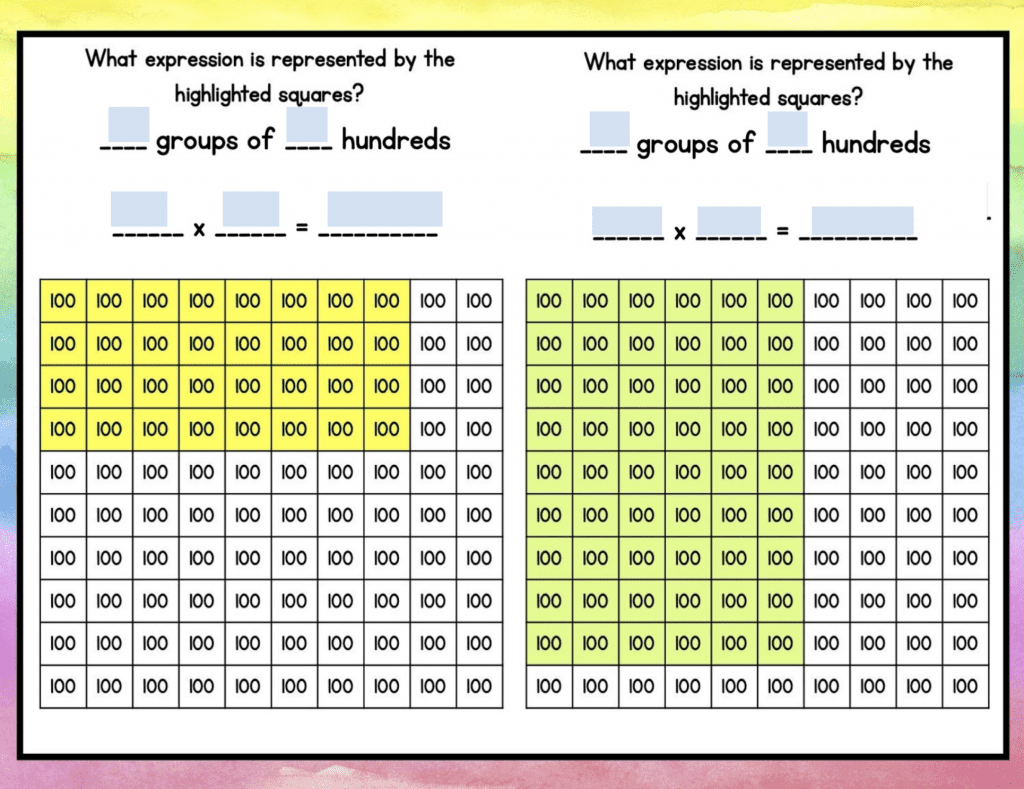
Students then build arrays to represent multiplying by multiples of 10 and 100. In the digital activity, students drag the place value circles to build the array.
To give students even more multi-digit multiplication exposure, students read arrays using multiples of 10 and 100. They also build arrays be highlighting the squares within the chart.
To shift students to more abstract understanding, students drag and drop numbers to complete the multiplication equation. Can you see how helpful this will be when students get to division?
Practice
Students can also use grid paper to represent their understanding of multiplying by multiples of 10 and 100. This lesson emphasizes how the associative property allows students to multiply by multiples of 10 and 100.
You will see this concept immediately click for some students, and you’ll have others who will need additional small group instruction.
Distributive Property & Multi-Digit Multiplication
Confession: when I was teaching third grade and the distributive property was added to my standards, I had no idea what it was! Even when I first taught it, I wasn’t sure why it was important. It took a bit to see just how powerful it was.
Introduction
A great way to review the distributive property is through a matching lesson. I give students a collection of arrays, and students work in a group to match the blue arrays with two green arrays that can be combined to have the same dimensions and product. For example, students may match 8×6 with (8×3) and (8×3). This helps students see how they can break larger multi-digit multiplication problems into 2 or 3 smaller ones.
Continued Practice
In a following distributive property lesson, students complete a cut and paste activity. Assign groups different multiplication problems and have students try to make as many arrays as possible to model how to use the distributive property to solve the problem. I like to display these posters in the hallway as evidence of what we’re learning in class, as well as to allow other students to see the variety of models.
You can follow the cut and paste lesson with an activity where students break apart multiplication problems on a small section of grid paper.
Making the Transition to Multi-Digit Multiplication
Once these foundations are developed, you can begin to transition students to larger, multi-digit multiplication problems.
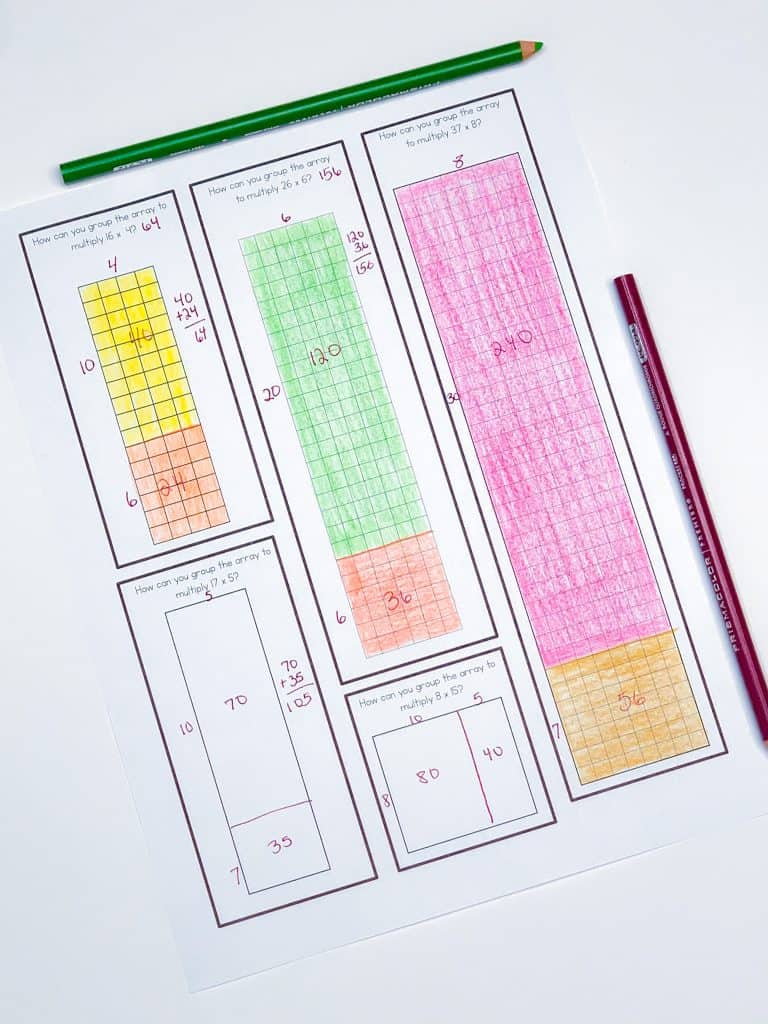
I often give students a large problem such as 346×7 without any guidance or instruction. I want to see what strategy they use to approach the problem. The results are often shocking, because many students instinctively go to partial product without having ever heard the term or seeing an example.
You can see in this example, how I slowly fade away the individual squares from the arrays to allow students to build area models. I like to over dramatize the annoyance of counting out all the squares and act as if using the area model will be SUCH a time saver.
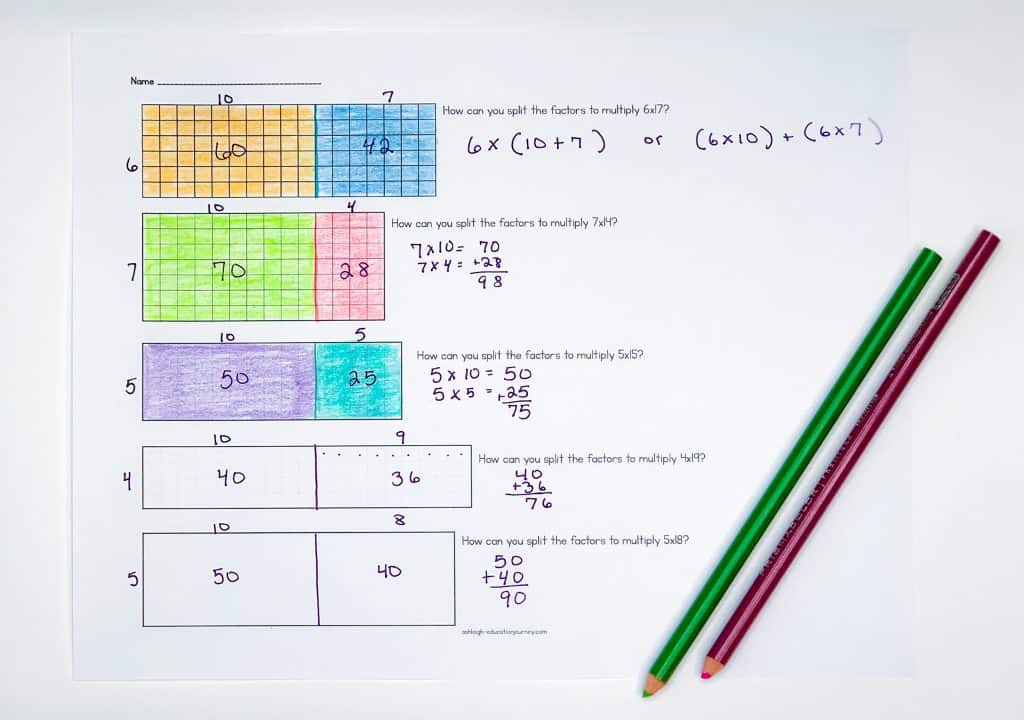As you introduce this to students, it’s important to not only use horizontal area models. Students should be flexible in their thinking and understanding and not view these models as just boxes or rectangles. They are a representation of an array. There should be meaning in the area models.
These transitional lessons make the “official” fourth grade multi-digit multiplication lessons so much easier-for you and your students!
