Multiplication Interventions

Multiplication interventions are incredibly important for students struggling in math. In third, fourth, and fifth grades, there are few math concepts more important for students than multiplication. This builds the foundation of multiple other math topics and concepts. However, many students need additional instruction and remediation during and/or after their multiplication unit. This blog post shares ideas that can be used for multiplication remediation or multiplication interventions that can be used with students who need extra support. These are not the same lessons that I teach in my multiplication unit. Instead, these are lessons I teach in addition to the lessons taught within my multiplication unit.

The multiplication intervention lessons begin very easy, but they build a conceptual understanding of multiplication that will later help students solve word problems with larger numbers. I’ve included each of these as a part of my Math Intervention resource. During this time, I do not focus on the memorization of multiplication facts. I don’t want to focus too much time on memorization and forfeit understanding. However, at other times I do focus on these facts, and you can read more about that here.

Concept of Multiplication Intervention Lessons

I like to begin by using a game to continue helping students understand the concept of multiplication. Students spin once to determine the number of groups they have, and again to determine how many are in each group. I have students build the group with manipulatives, draw the groups with a pictorial representation, or use a symbolic representation. With each turn, I make sure students understand the difference between the number of groups and how many are in each group.

It’s also important to show students models of multiplication problems and have students determine which multiplication fact the model shows. I do this through manipulatives and pictorial representations. This time spent working with equal groups will allow student to understand the meaning of multiplication.

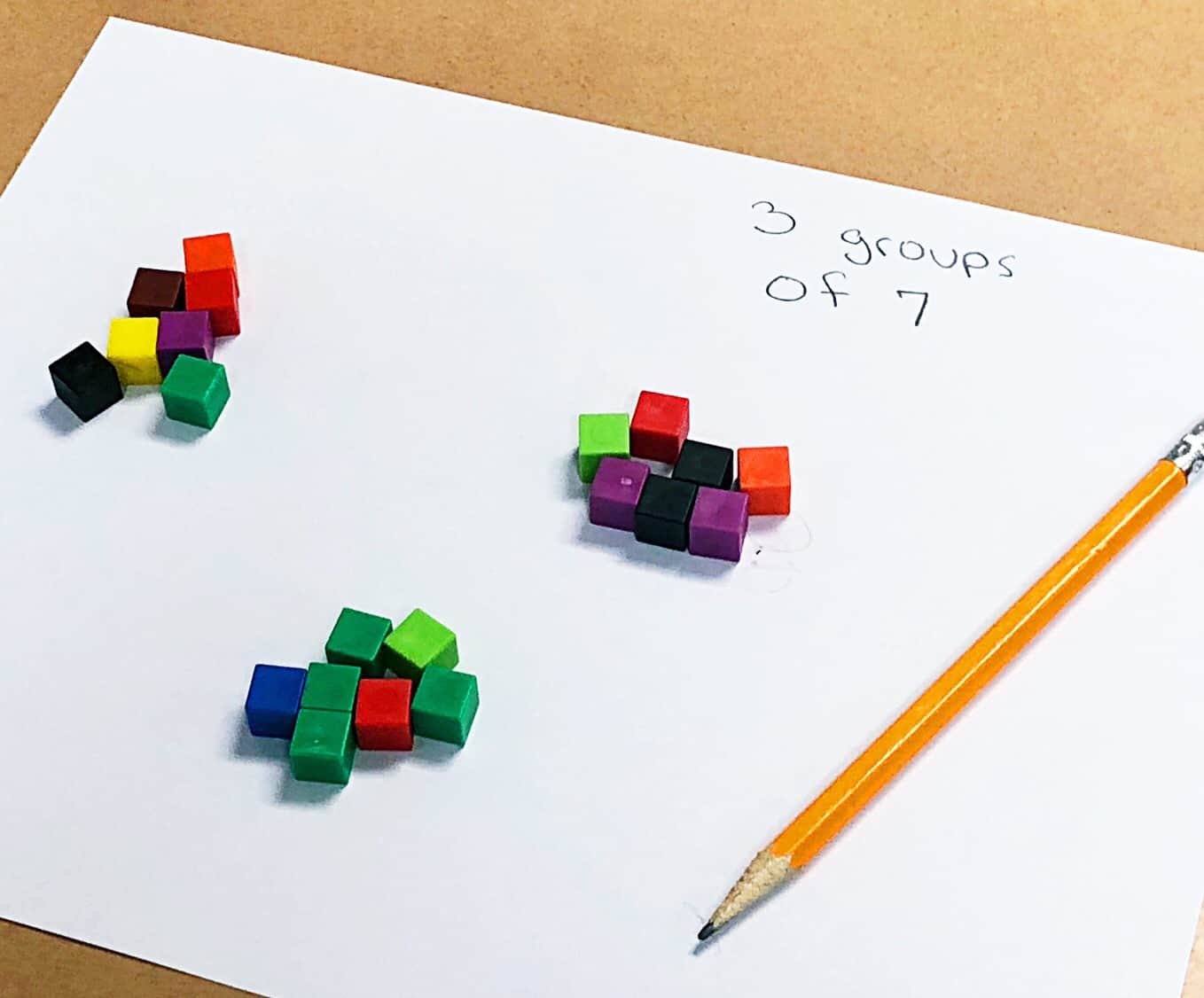
When teaching about the meaning of multiplication during your multiplication intervention lessons, it is also necessary to spend a considerable amount of time teaching students how to correctly create and read arrays. I’ve found that many students try to create a top row and a left column but leave all the middle pieces. This shows yet another misconception. After students have an understanding of arrays, we work to build all of the arrays possible for numbers 1-24. This will be a great lesson to refer to when teaching about prime and composite numbers. A solid understanding of arrays will also be a tremendous help for students when they begin to use the distributive property to solve larger multiplication problems.

Another multiplication intervention activity that allows students to see patterns within multiplication is to have students place counters on a number line to show the multiples of different numbers. Ask students to predict what other numbers would be marked if the skip-counting continued. Ex: “When skip-counting by twos, will the number 127 have a peg?  You can also have students mark two sets of multiples on the same number line, for example, multiples of three and six. Some numbers will have two counters on them.

It’s also important to give students the opportunity to work with a multiplication table. Have students use the grid paper to build and cut out all the possible arrays for 12 and write the multiplication equation inside the array. Have students place the 4×3 array on the chart so that the upper-left corner of the rectangle lies on the upper-left corner of the chart. Students should hold the rectangle in place as they count the squares. Then have students lift the lower-right corner of the rectangle to show the product 12.

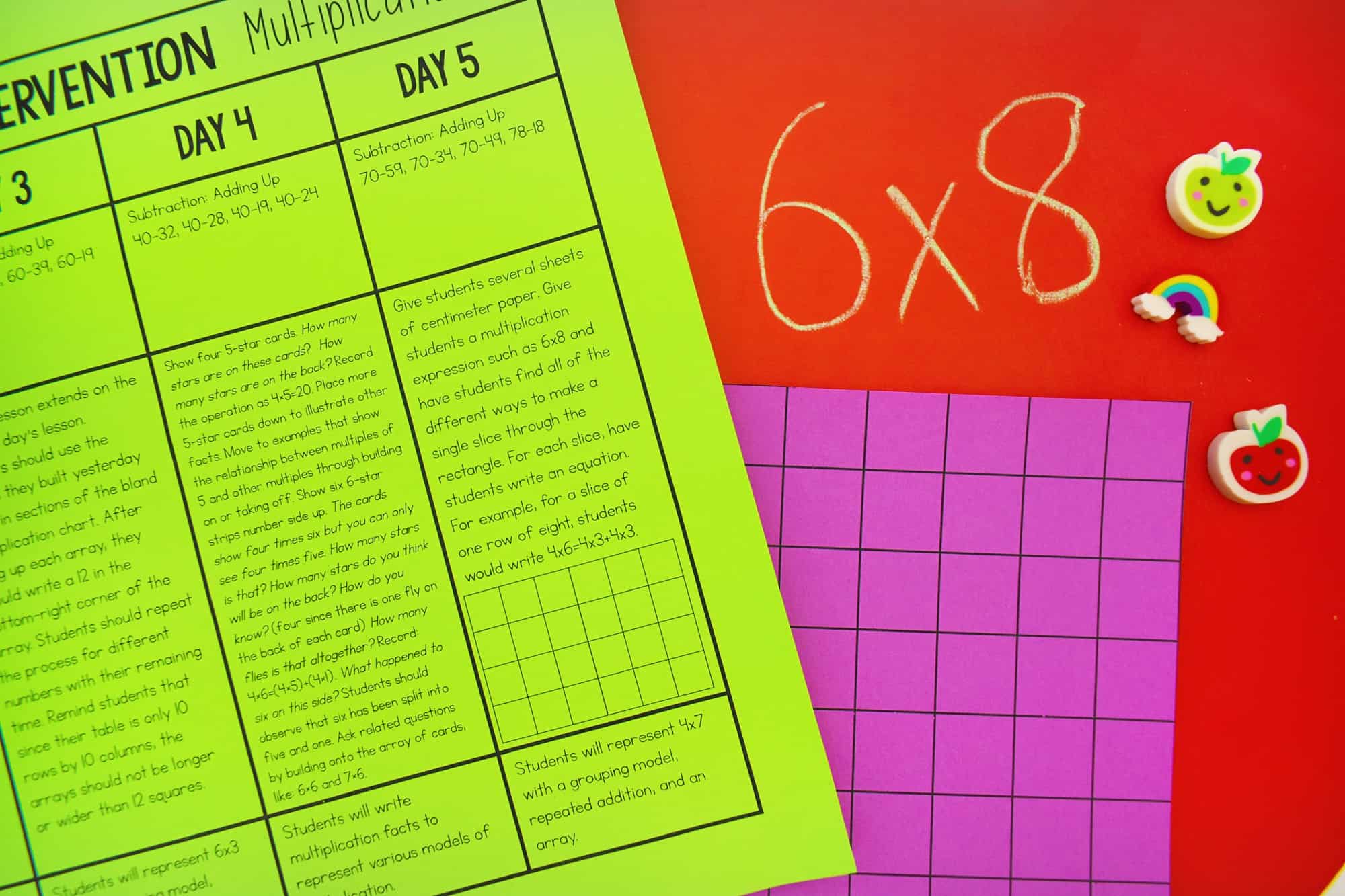
As students work with grid paper and multiplication tables, they will begin to see how multiplication problems can be broken into smaller problems. A great way to reinforce this is to give students a multiplication expression such as 6×8  as an array on grid paper and have students find all of the different ways to make a single slice through the rectangle. For each slice, have students write an equation. For example, students would write 4×6=4×3+4×3.

Multiples of Ten

At this point, students are typically ready for more challenging multiplication concepts, so I then begin to teach students to multiply by tens and eventually multiples of ten. One way to teach this is through money, so I like having students multiply using pretend $10 bills. I also teach students to solve multiplication problems that have three factors. We model how to pair two factors and find their product and then multiply again to find the product. I like to model how to multiply using all three possibilities, which allows great multiplication conversations. This is another activity that’s easily turned into a game for students.

In another multiplication intervention lesson, students reverse what they learned and turn 2-factor problems into 3-factor problems. To teach this, show students the problem 4×30 and model how to solve as 4x3x10. Ask students to explain why they think you chose to save 10 for last. Repeat with 4×300. Ask students why factor they could save for last. This skill will be a tremendous help for students when they begin to solve more challenging math problems.

Multi Digit Multiplication Interventions

I then like to teach students how to use the distributive property to solve 2-digit multiplication problems with an array. Eventually, students will solve these problems using an area model, so I slowly scaffold away, by fading, the interior squares in the array. As the squares fade, students grow less dependent on the model.

To move students toward larger multiplication problems, present students with a 3-digit by one-digit problem such as 4×384. Ask students if it would make sense to literally draw an array with 4 rows of 384. Since we know that would take too long, ask students what their other options are. Guide students into understanding they can draw the outline of the array and break it into parts. Model how to break apart 384 into 300+80+4 and how to multiply each part by 4. Repeat this process until you feel that students are comfortable breaking apart the numbers.

In the multiplication intervention lessons, I like to have students begin 2-digit by 2-digit multiplication by multiplying multiples of ten, and then I move students into using grid paper to create area models for solving these multiplication problems. Since this is often challenging for students, I like to incorporate base-ten blocks into my instruction. This helps eliminate misconceptions and common errors.

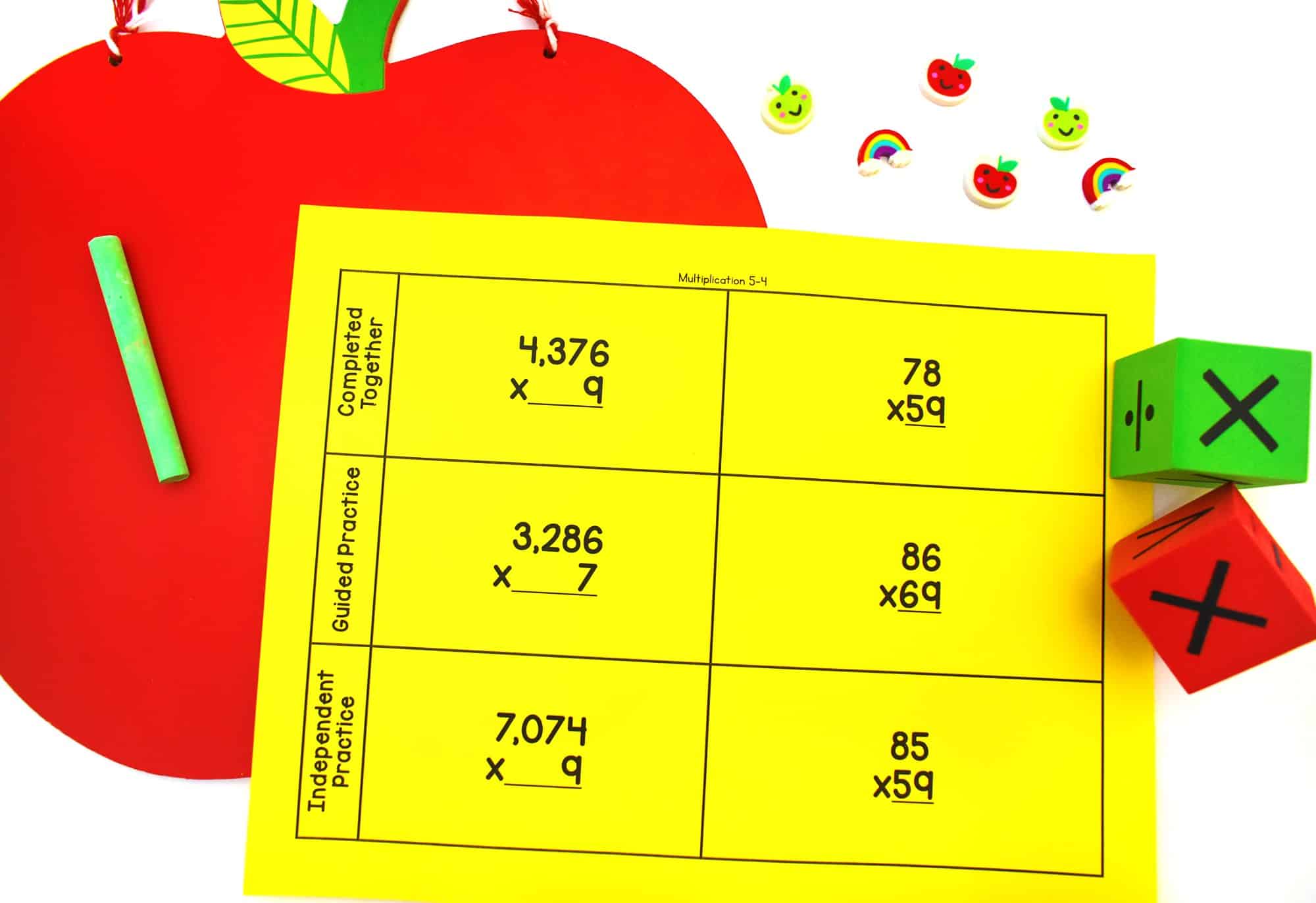
Toward the end of my multiplication intervention lessons, I teach students how to solve problems with partial product and/or the algorithm. I like to have students complete two problems together, complete two more through guided practice, and then complete two independently. This allows me to see where to progress from that day’s lesson.

Each of the lessons in this post are a small part of my Upper Elementary Math Intervention resource. It has been such a game-changer for me! Also, each lesson includes a very brief exit slip that allows you to monitor and track student progress.

You can read more about the organization and implementation of math interventions here. Please let me know if you have any questions!