When you teach upper elementary math, teaching addition and subtraction can be….awkward. Generally speaking, your students already understand the concept. Whether you want them to or not, they know and use the standard algorithm. Of course, there are some students who have not yet mastered the algorithm, and those students need small group instruction. But what about the whole class? Where do you begin instruction? Should you skip teaching addition and subtraction and save time for other concepts?
I like to spend about a week teaching addition and subtraction. Yes, that’s fast. At the beginning of the year, I give an addition and subtraction pretest. I use that data to pinpoint who needs extra support.
I write the names of students who need extra support and start at the top of the page. I gradually work my way down the different types of problems. Ideally, by the time I begin the actual unit, the majority of students have mastered the algorithm.
I recognize that there are a lot of theories and research of how and when the standard algorithm should be introduced, but in reality most students will be familiar with it by the time they are in third, fourth, and fifth grade. I do teach other addition and subtraction strategies through number talks, but I don’t extend our addition and subtraction unit for those strategies.
Instead, I use our week teaching addition and subtraction to focus on word problems. In this post, I’ve shared how I introduce and teach addition and subtraction word problems and how I continue to reinforce the concept of place value within these lessons. Each of the lessons below are from my 4th Grade Addition and Subtraction Unit.
Action and Nonaction Word Problems
Word problems are extremely important in allowing students to make sense of math through real world context. In this first addition and subtraction lesson, students begin to make sense of the structure of word problems.
Give students a collection of word problems and have students sort the word problems into two groups. They may use any grouping that makes sense to them. Ask students to share how they sorted the word problems.
More than likely, the most common approach will be addition and subtraction. Ask students how they determined the operation and have students share how they determined the operation. Ask students if they can find or think of an example of how over-relying on key words could result in an incorrect answer. Use that conversation as a starting place to emphasize the importance of understanding word problems.
Explain to students that one of the keys to understanding word problem is to recognize action and nonaction word problems. Action does not necessarily refer to movement but that something happens to the initial quantity in the problem. This is a great time to have students take turns acting out various word problems.
After students are familiar with this idea, have students resort their cards into action word problems and nonaction word problems. Have students complete the Action or Nonaction Word Problems sheet. In this practice page, students solve six addition and subtraction word problems. Then, they shade in the word problems that show action with green and the nonaction word problems with red.
This may seem like an overly simplistic lessons, but it begins to build a foundation for more specific types of word problems. It’s best to not overwhelm students with too much, too soon.
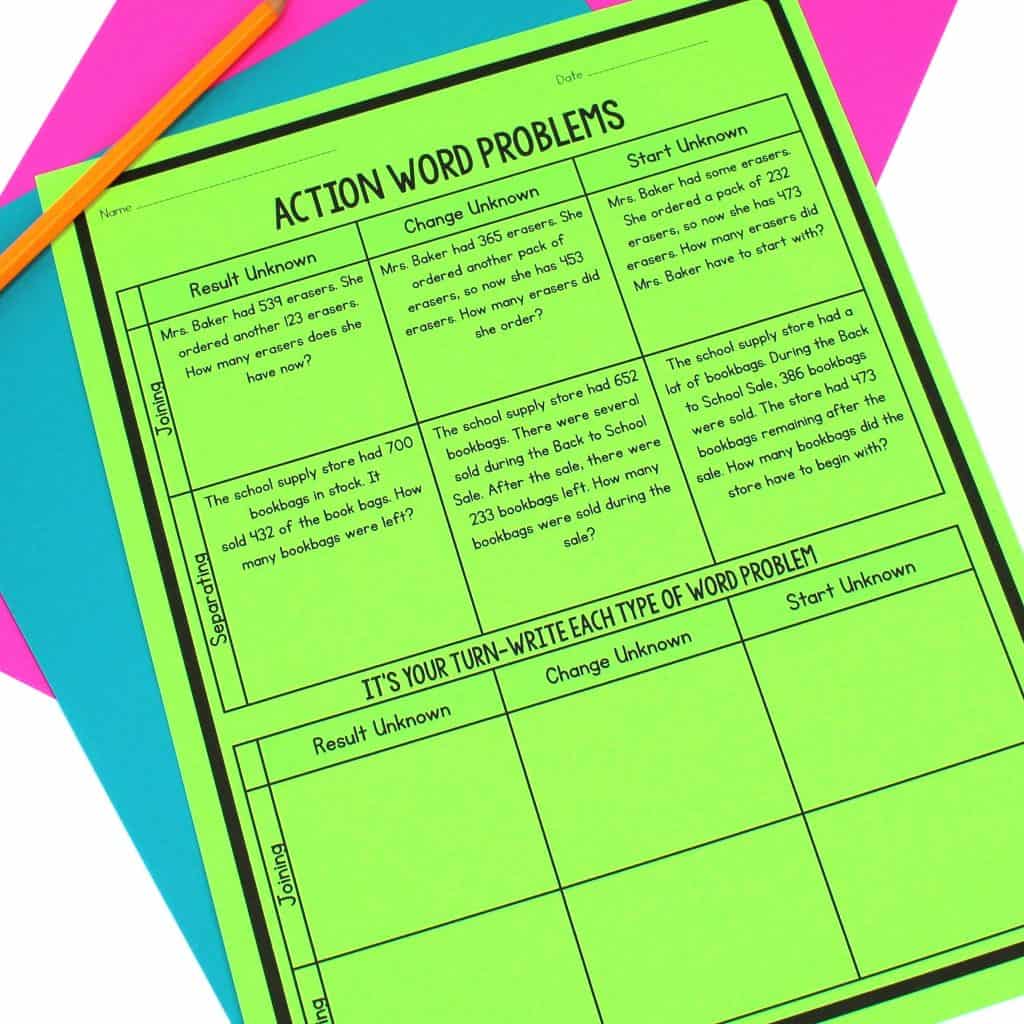
Types of Action Word Problems
In this lesson, students can reuse the sorting cards from the previous lesson. Have students sort the action cards into joining and separating problems. This step should be somewhat easy for students.
After students sort their cards, introduce the terms ”result unknown” “change unknown” and “start unknown”. Go through each of the cards to determine what type of unknown the card includes. The “change unknown” card in the joining problem is often overlooked by students as the action is implied.
Place six sheets of chart paper around the classroom. Label each sheet of chart paper with: Joining Start Unknown, Joining Change Unknown, Joining Result Unknown, Removing Start Unknown, Removing Change Unknown, Removing Result Unknown.
Have students write an example of each type of word problem on a separate sticky note. After writing the word problems, students should place the sticky notes on the corresponding sheet of chart paper. For extra practice, students can complete the Types of Action Word Problems worksheet.
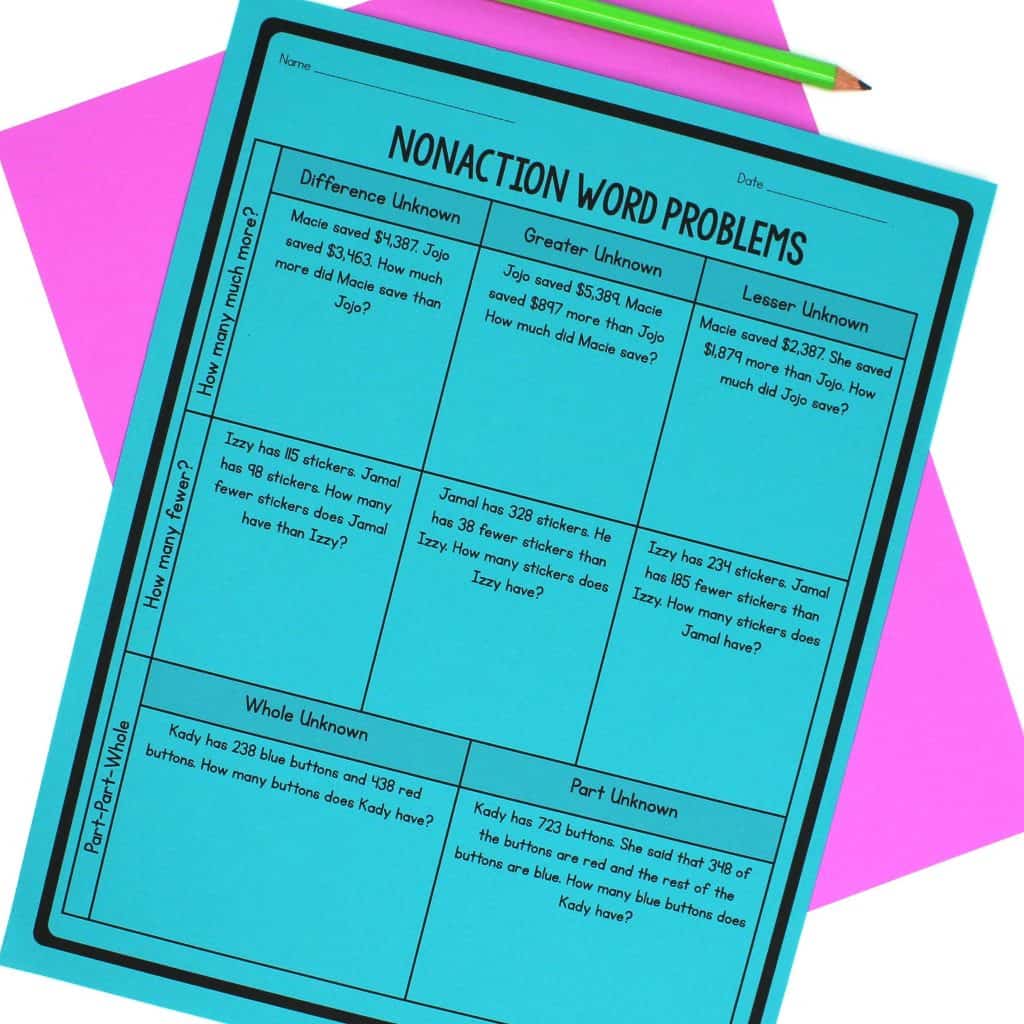
Types of Nonaction Word Problems
In the next lesson students begin to learn about nonaction word problems. Have students take out the Nonaction Sorting Cards and place those cards into two groups. Give students time to discuss how they determined how to sort their cards.
Explain that one way to sort the cards is by type of nonaction word problems. These word problems consist of comparison situations and parts and wholes. Give students a few examples of each time of problem and then have students resort the cards by comparison and parts and wholes.
Place five sheets of chart paper around the classroom. Label each sheet of chart paper with: Comparing Difference Unknown, Comparing Greater Unknown, Comparing Fewer Unknown, Part-Part-Whole Whole Unknown, and Part-Part-Whole Part Unknown.
Have students write an example of each type of word problem on a separate sticky note. After writing the word problems, students should place the sticky notes on the corresponding sheet of chart paper.
For extra practice, students can complete the Types of Nonaction Word Problems worksheet.
Situational Equations
This is a really important lesson. Connecting different types of equations supports the connection between the structure of the word problem and the process of determining a solution. Many times when students write equations, they write an equation that can be used to solve the problem, but it does not represent the situation of the word problem. Situation equations represent the action of the problem. Solution equations can be used to solve the problem. Some equations can be both a situation equation and a solution equation.
Example: Some children were playing tag at recess. When another class came outside, eight more students joined them. Now there are 14 students playing tag. How many students were playing tag to begin with?
The solution equation would be 14-8=_____. However, the situation equation is ____ + 8=14. This can also be a solution equation.
Go through each type of action word problem and have students notice the placement of each unknown quantity for each problem. Students should recognize that the unknown quantity naming the word problem also describes the location of the unknown in the situation equation.
Then discuss what type of solution equation would be most effective to solve the problem. Students may vary in their choices for this portion.
Explaining the Algorithm
When teaching the standard algorithm, it’s important to talk about the process so students can make connections between concepts of place value and the steps involved in the algorithm. Use the language below to explain the algorithm for addition and subtraction.
Addition
- When you add 7 ones and 9 ones you get 16 ones.
- Trade ten ones for 1 ten and 6 ones.
- Write the 1 ten above the tens column and the 6 ones in the answer space of the ones column.
- Three tens, plus 8 tens, plus 1 ten is 12 tens.
- Trade 10 tens for 1 hundred, and then you have 1 hundred and 2 tens.
- Write the 1 hundred above the hundreds column and the 2 tens in the answer space for the tens column.
- Two hundreds, plus 3 hundreds, plus 1 hundred is 6 hundreds.
- Write the 6 hundreds in the answer space for the hundreds column.
Subtraction
- Beginning with the ones place, take 2 ones from 6 ones, leaving 4 ones.
- Write the answer in the ones answer column.
- In the tens column, there are not enough tens to take away 8 tens, so trade 1 hundred for 10 tens. That leaves 3 hundreds and 13 tens.
- Now, take 8 tens away from 13 fens, which leaves 5 tens.
- Write the answer in the tens column.
- Take away 2 hundreds from 3 hundreds, which leaves 1 hundred.
- Write the 1 in the hundreds column answer space.
It’s also important to give students time to work with base ten blocks to clarify the standard algorithms.
Finally, never underestimate the power of writing about math. It’s hard. It’s time consuming. It’s worth it. Have students use their own words to explain the addition and subtraction algorithm.
After I teach these lessons, I revisit the algorithm and word problems all year long, so it’s not horrible if there are some students who need extra time. They will absolutely get that time and support. I also teach additional strategies through our math warm-ups. However, as far as our class pacing, after this week’s instruction we are ready to move forward.
To give you even more resources for teaching addition and subtraction, I’ve included this free resource that incorporates problem solving, estimation, addition and subtraction.