Most teachers begin the year by teaching place value. That isn’t a coincidence. We begin with place value because it lays the foundation of all additional math concepts. Unfortunately, teaching place value can be tricky, and it’s easy for students to fake understanding. That’s why it’s so important to slow down and teach for a deep understanding.

In this post, I’ve shared lessons you can use for teaching place value and how to read write different forms of numbers. Each of these lessons are from my Fourth Grade Place Value Unit. You can read more about third grade place value here.

Place Value Houses

While I love teaching math through problem based learning and focus on lessons that require application, I can’t jump in too fast. Before beginning more advanced lessons, students must first understand place value conventions and terminology. That’s why I use place value houses as a general introduction to teaching place value.

To understand our base-ten system students must understand that ten in any position makes a single unit in the next position. You can use base ten blocks to guide students into understanding that one unit represents one and that ten ones grouped together make a tens. Be sure to discuss how this continues with hundreds, thousands, ten thousands, and hundred thousands.

To move students from a concrete model to a pictorial representation, they construct houses to represent the ones, thousands, and millions periods. Students cut out the houses and glue them on a sheet of white construction paper. They can later add decorations and details. In each house, students record how many ones, tens, hundreds, etc. are in each place.

Building Numbers

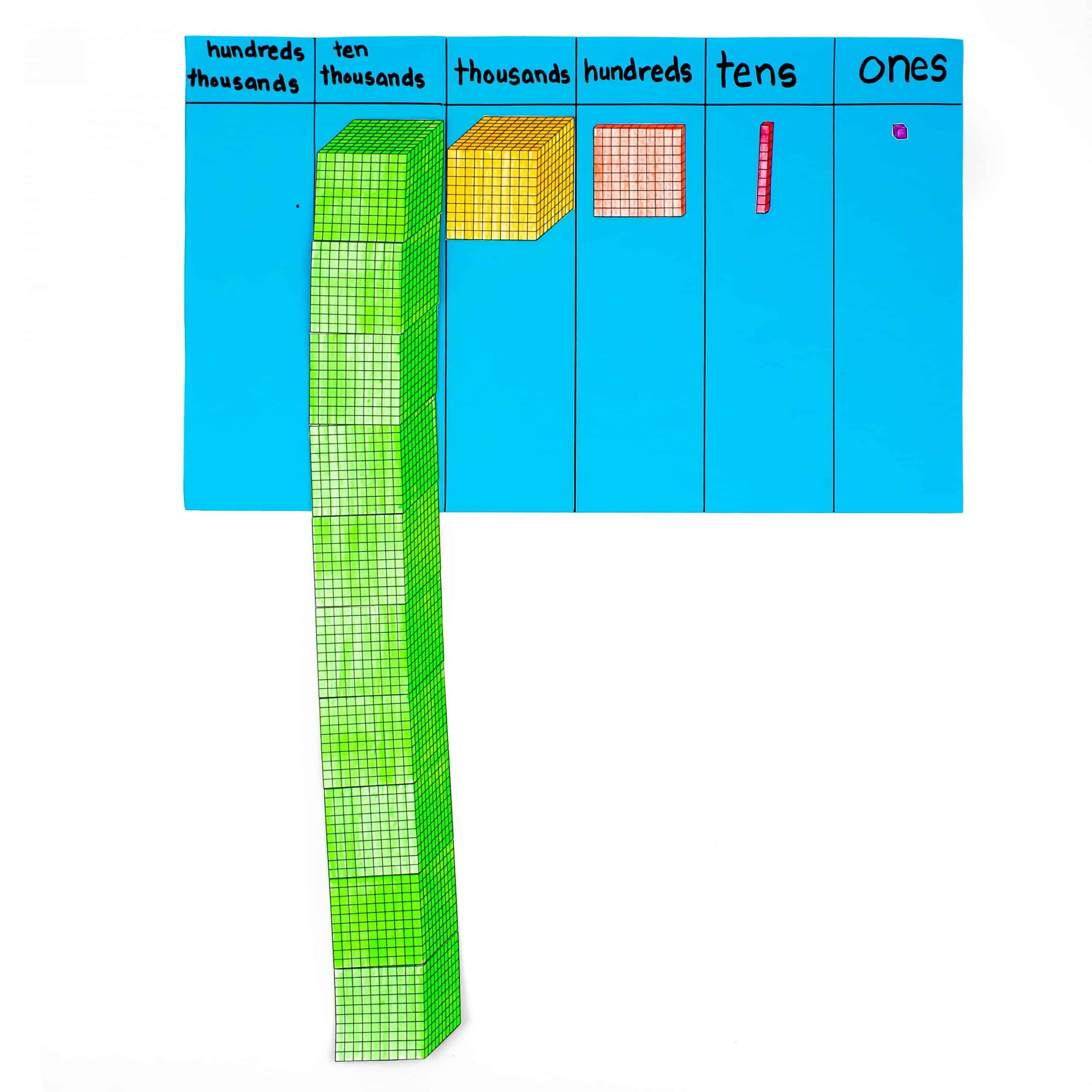
As students begin to develop a more conceptual understanding of our base-ten system, they will begin to understand the relative size of each place. Have students cut out a ones block and glue the place value block in the ones place. Discuss how ten ones builds a ten and have students cut out and glue the tens rod to the tens place. Repeat for the hundreds place.

Things get interesting when you get to the thousands place. Students should realize they can place 10 hundreds together to build a thousand. Have students cut out the ten 100s blocks and glue them together underneath the thousands place. You can repeat with the ten thousands place. Since that place value is so large, students will tape the blocks together to make a long chain.

Of course you can keep going to the hundred thousands place, or even millions place, but that will be pretty time consuming. You could even use one portion of your hallway for that model.

Base Ten Problems

This lesson lets students work with concrete, pictorial, and abstract versions of numbers. When completing the first portion of the task, students should use base-ten materials. This allows students to become more flexible in their place value understanding and application. Since most teachers don’t have access to such a large quantity of base-ten blocks, you may use the place value table and small counters for students to build their numbers.

In the next portion of the lesson, students use a pictorial representation. As you discuss the problems with students, begin to introduce an abstract representation of the number.

In the final this portion of the lesson, students try to solve the problem without using concrete materials or pictorial representations. Instead, they should use abstract representations.

Naming Numbers

I love using place value chips when teaching place value. I use these rather than base-ten blocks, because it’s next to impossible to build six digit numbers using base-ten blocks. These are much smaller, convenient to store, and they’re quiet! Write numbers on your dry erase board and have students use their place value chips to build the number.

Once students understand the concrete version of this model, they can transfer that to a pictorial understanding by using the printable below. The first three problems have students shade in place value discs to represent different numbers. The next two problems have students identify numbers based on what is already shaded in. Some questions require students to think a little deeper and apply the regrouping principle to the different values of the numbers.

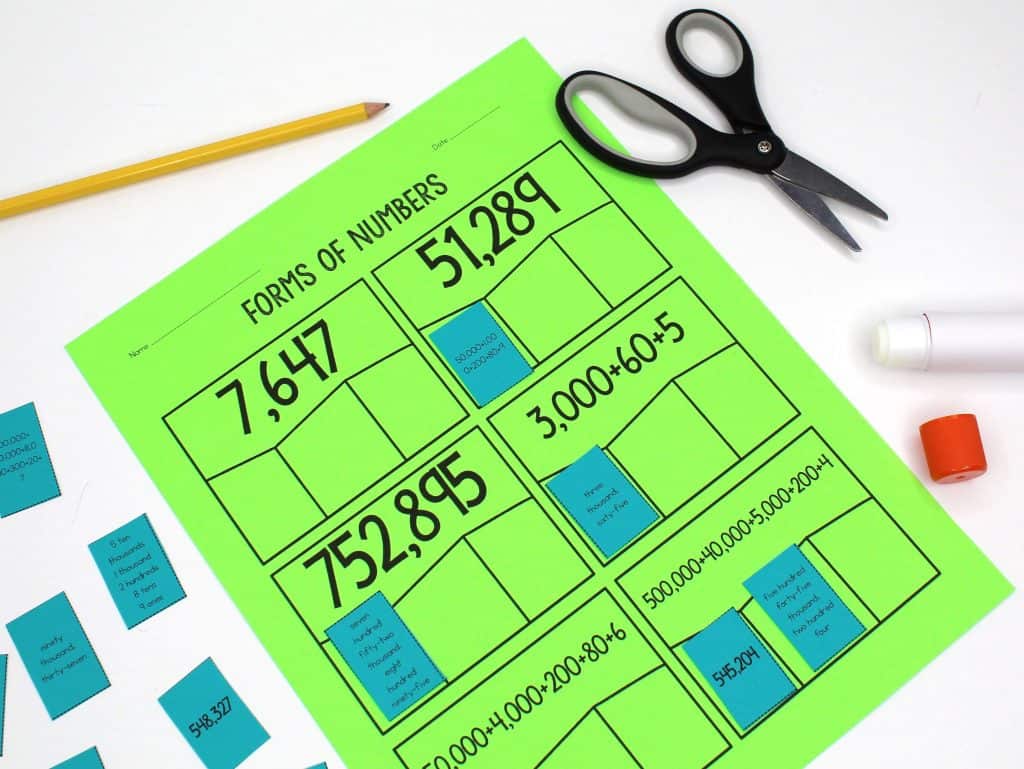
Forms of Numbers

I’ve found that learning to read and say the numbers was a bit of a challenge for some students, so we start there and moved forward. Students use their dry erase boards and place value chips to practice writing different forms of numbers. Zeroes often confuse students when they’re trying to follow a procedure with memorized steps, so always be on the lookout for that error.

To follow that mini lesson, students complete the place value puzzles. In the activity, students match numbers written in standard, written, and expanded form to fit the puzzle pieces together.

Roll a Number

More than likely some students will need a little extra time before moving forward in your place value instruction. That’s when I love incorporating games. This gives me flexibility to meet with small groups for additional instruction while other students enrich their understanding.

Representing Numbers Anchor Chart

While teaching place value, I display my Math Anchor Charts . No matter how hard I try, trace, measure, outline…you name it….I cannot make a nice looking anchor chart, so I hang these up for my students to reference throughout the year. I also have a third grade version of the anchor charts.

Teaching Place Value

Have you ever read a standard where you had to read and reread to understanding the wording of a standard? That’s how I felt when I first read 4.NBT.1 Recognize that in a multi-digit whole number, a digit in one place represents ten times what it represents in the place to its right. 

This is one of those standards that seems so intuitive to many of us as adults, but it’s incredibly abstract and confusing to students. However, it’s one of those essential math concepts that students need to fully understand.

Ten Times Larger: An Introduction

When introducing this concept about the value of digits, refer back to the place value chart where students built representations of 1, 10, 100, 1,000, 10,000 and even 100,000. Use the visual to explain that one ten is 10 times as much as 1 one. Repeat with tens to hundreds, hundreds to thousands, thousands to ten-thousands, and ten-thousands to hundred-thousands. This visualization will help students understand that the unit on the left is 10 times as many as the current place.

The same strategy can be used for showing students what is 100 times bigger or even 1,000 times larger. While this does go above most fourth grade students this tends to solidify students’ understanding on how numbers increase based on their place value position.

Follow the explanation above with this hands-on activity. Students will cut out arrows that are labeled 10x bigger, 100x bigger, and 1,000x bigger. Students will use those arrows to determine how much larger same digits are within given numbers.

For example, in this problem students create the number 614,277 and determine how many times larger is the 7 in the tens place than the 7 in the ones place. Students can cut out individual digit cards or they can cover the top portion with a page protector and write with a dry erase marker.

This is such a useful way to guide students into this complex concept. Students repeat this with a collection of numbers. As an extension, have students determine what number to create. For example, Build a number where the 6 in the hundreds place is ten times bigger than the six in the tens place.

Place Value and Number Lines

The length and focus of this place value lesson will be dependent on your students’ past experiences with number lines. If they have not used number lines in previous grades, you will need to spend teaching students how to use a number line.

In this problem-solving task students determine the increments on two number lines. The first number line is 200 and the second is 225. Have students label the tic marks on the number lines using those intervals. Then, using the numeral digits (numbers can be used more than once) students should build possible numbers for Point A, Point B, and Point C. There are several possible answers for this problem and the open ended nature of this task provides excellent math conversations.

Comparing on a Number Line

It’s beneficial to frequently incorporate number lines into your instruction. They’re a great resource for teaching students to compare numbers. This will come back in when students compare decimals. When teaching place value, work with students to write comparison statements with symbols for various five and six-digit numbers. Have students note the greatest place value position that is different is what allows them to see which number is greater.

It’s also good to incorporate problem solving tasks as you teach comparing numbers. It’s a great way to get students thinking.

Comparison Statements

Many students also need to develop an understanding of what comparison statements actually mean. I’ve found that some students repeat what I say, often correctly, but they don’t know what it means. That’s why in this next lesson, students use the concept of 10 times bigger, 100 times bigger, to develop an understanding of those comparison statements.

In this task, students use the animal pictures to answer questions related to the comparative value of each digit. They begin with writing three 10 times larger statements and then three 100 times larger statements. At the end of the task students solve problems such as:

• The __________________________ is 100 times larger than the hummingbird.
• The tree boa is 100 times larger than the __________________________.
• The __________________________ is 1,000 times larger than the butterfly.
• The sloth is 10 times larger than the __________________________.

Teaching Place Value – Comparing Numbers

While teaching place value, it’s a great time to teach comparing numbers. I have students complete another page in the math notebook, and I’m careful to make sure students can tell the place value of the digit that was used to compare the numbers.

After introducing how to compare numbers and reviewing the comparison symbols, students complete a practice activity. To make this a little more interactive, I added two spinners. Students use a paperclip to spin one time on each spinner to find two numbers to compare. They write the number in the table and then write a comparison statement.

The second page is a little more advanced because the numbers aren’t written in standard form. Instead, they’re written in written form, expanded form, expanded notation, and some are even written where students will need to regroup.

Ordering Numbers

After I teach comparing numbers, I like to also teach a lesson where students order numbers from least to greatest and greatest to least. I created a sports related activity for students. What makes it special is that I got the information from the children’s book The Economics of the Super Bowl.

What makes it even cooler is that students can read the book for free on Epic. However, in the text the numbers are already in order, so you may want to wait and use the book as a self checking strategy.

Teaching Place Value – Expanded Notation

Expanded notation is not specifically mentioned in all state’s fourth grade standards. Even though it’s not included in my students’ standards, I still like to introduce the concept to students while teaching place value. This is just another step to help students see place value and the value of digits within numbers.

I use the same process as above for the mini lesson, and I add expanded notation into the conversation. Then I give students this adorable follow-up activity.

Below is a digital example of the activity. Students use the values of each individual component to an ice cream cone to determine each cone’s total value. I have students write that value using expanded notation AND numeral form.

The second part of the activity is a bit more fun and a bit more challenging. Students are given a total and must drag and drop the ice cream pieces to build an ice cream cone with the given value. If you use the print version, students will be able to draw, rather than drag and drop.

 

Each of the lessons above are a portion of my 4th Grade Place Value Unit.

Teaching Place Value – Anchor Charts

After finishing the unit, I hang up my Math Anchor Charts that are a bit smaller than my anchor charts. No matter how hard I try, trace, measure, outline…you name it….I cannot make a nice looking anchor chart, so I hang these up for my students to reference throughout the year. I display the chart when I begin teaching place value and leave it displayed on an as-needed basis. I also have a third grade version of the anchor charts.

Teaching Place Value – Extra Practice

Just in case you need it, I included a skills practice printable the corresponds to each of the lessons. The pages range from representing numbers, place value, comparing numbers, size of numbers, and rounding.

The included games are also great for teaching place value through math work stations or math centers.