
Have you ever read a standard where you had to read, reread, and reread again, and you were still completely confused? That’s how I felt when I first read 4.NBT.1 Recognize that in a multi-digit whole number, a digit in one place represents ten times what it represents in the place to its right. While I understood the concept, I had a hard time visualizing how to teach this concept on the value of digits to my students.
This is one of those standards that seems so intuitive to many of us as adults, but it’s incredibly abstract and confusing to students. However, it’s one of those essential math concepts that students need to fully understand.
In this post, I’ve shared some of my favorite lessons and activities for teaching the concept and value of digits so students get it and remember it. You can find all of these lessons in my 4th Grade Place Value Unit.
In this post:
- Ten Times Larger: An Introduction
- Multiplying by Multiples of Ten
- Comparison Statements
- Comparing Numbers
- Ordering Numbers
- Distance Learning
- Anchor Charts
Ten Times Larger: An Introduction
Students’ previous lessons on place value laid the foundation for this concept. You can read more about those foundational lessons in this place value post.
When introducing this concept about the value of digits, refer back to the place value chart where students built representations of 1, 10, 100, 1,000, 10,000 and even 100,000. Use the visual to explain that one ten is 10 times as much as 1 one. Repeat with tens to hundreds, hundreds to thousands, thousands to ten-thousands, and ten-thousands to hundred-thousands. This visualization will help students understand that the unit on the left is 10 times as many as the current place.
The same strategy can be used for showing students what is 100 times bigger or even 1,000 times larger. While this does go above most fourth grade students this tends to solidify students’ understanding on how numbers increase based on their place value position.
Follow the explanation above with this hands-on activity. Students will cut out arrows that are labeled 10x bigger, 100x bigger, and 1,000x bigger. Students will use those arrows to determine how much larger same digits are within given numbers.
For example, in this problem students create the number 614,277 and determine how many times larger is the 7 in the tens place than the 7 in the ones place. Students can cut out individual digit cards or they can cover the top portion with a page protector and write with a dry erase marker.

Then in this example, students build the number 511,510 and determine how many times larger is the 5 in the hundred thousands place than the 5 in the hundreds place. This is such a useful way to guide students into this complex concept.

Students repeat this with a collection of numbers. As an extension, have students determine what number to create. For example, Build a number where the 6 in the hundreds place is ten times bigger than the six in the tens place.
Multiplying by Multiples of Ten
I will never understand why multiplying by multiples of ten is so hard for students. As an adult, it seems so instinctive, but that’s not the case for many of our students. That’s one of the reasons so many students later struggle with multi-digit multiplication and division.
To review the previous lessons, students complete the Value of Numbers page in their math notebooks. (The Value of Numbers Form is in my TpT Store.)

Then we move into multiplying by tens and hundreds. This is not the only time I teach this concept, but I like to insert this concept within our place value lessons so students can see the connection between multiples of ten and place value.
There are so many ways to teach this lesson! It really depends on what resources you have and your students. The key is to allow students to move from concrete, to pictorial representations, and then to abstract computation. Far too often, we skip a step or two with this concept.
One strategy to teach this concept and reinforce the value of digits is to use base-ten chips or counters. These are an inexpensive alternative to base-ten blocks.
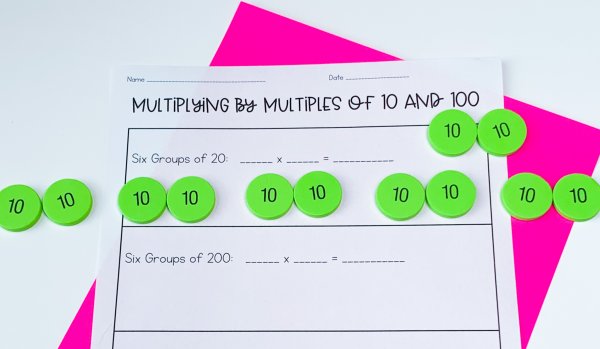
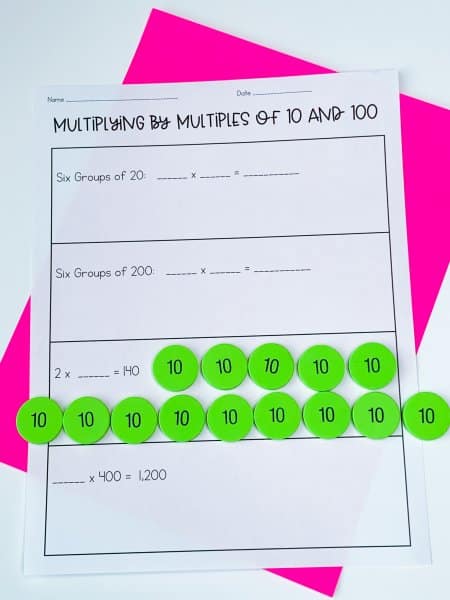
Of course, if you have base-ten blocks available, they are a great tool.

I’ve even tried base-ten stickers. The idea was great, but they didn’t work well for us. The hundreds stickers were way too big. However, the tens were easy for students to work with.

After students have ample hands-on experience, they can then move into pictorial models. Once again, there are several options.
The easiest is to have students draw the models. However, drawing makes it incredibly hard to think about proportions. I tried my best on this example, but I struggle-I really do!
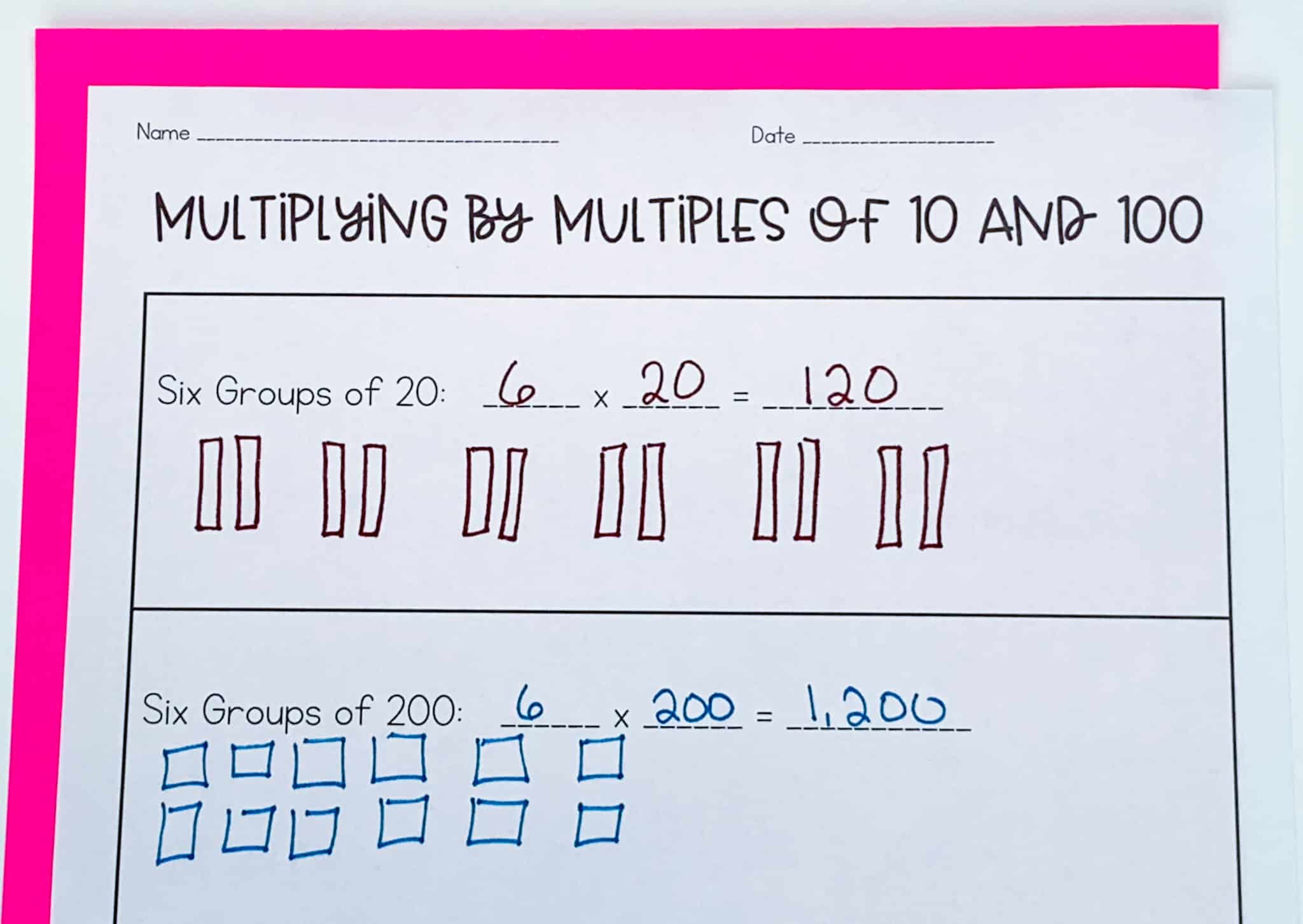
At this point, students aren’t ready to move into the abstract portion of multiplying by multiples of ten and hundred, and that’s okay. Most need that time to process this information.
Comparison Statements
Many students also need to develop an understanding of what comparison statements actually mean. I’ve found that some students repeat what I say, often correctly, but they don’t know what it means. That’s why in this next lesson, students use the concept of 10 times bigger, 100 times bigger, to develop an understanding of those comparison statements.
In this task, students use the animal pictures to answer questions related to the comparative value of each digit. They begin with writing three 10 times larger statements and then three 100 times larger statements. At the end of the task students solve problems such as:
- The __________________________ is 100 times larger than the hummingbird.
- The tree boa is 100 times larger than the __________________________.
- The __________________________ is 1,000 times larger than the butterfly.
- The sloth is 10 times larger than the __________________________.

Comparing Numbers
As students are learning about the size of each place and the value of digits, it’s a great time to teach comparing numbers. I have students complete another page in the math notebook, and I’m careful to make sure students can tell the place value of the digit that was used to compare the numbers.

After introducing how to compare numbers and reviewing the comparison symbols, students complete a practice activity. To make this a little more interactive, I added two spinners. Students use a paperclip to spin one time on each spinner to find two numbers to compare. They write the number in the table and then write a comparison statement.

The second page is a little more advanced because the numbers aren’t written in standard form. Instead, they’re written in written form, expanded form, expanded notation, and some are even written where students will need to regroup.
Ordering Numbers
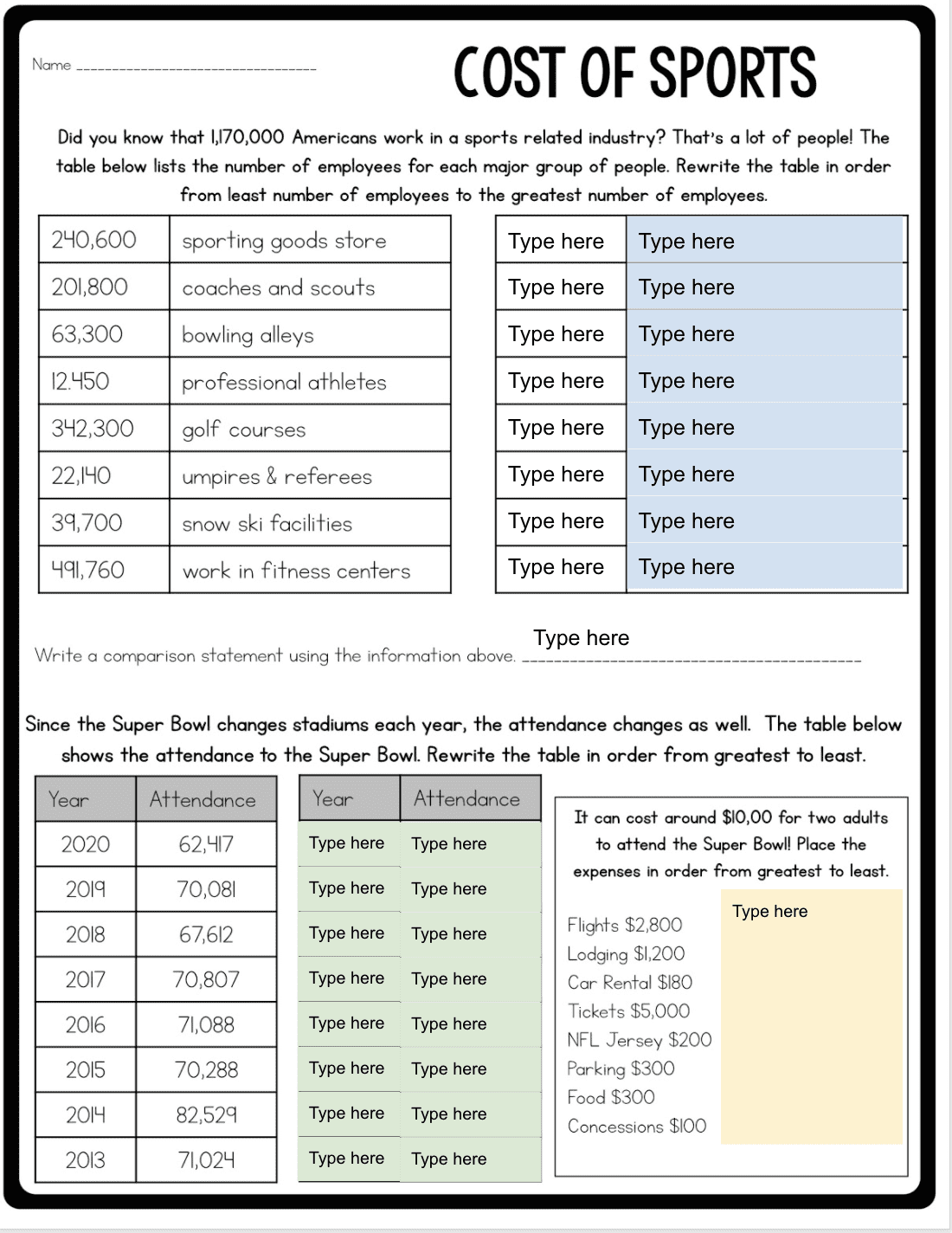
After I teach comparing numbers, I like to also teach a lesson where students order numbers from least to greatest and greatest to least. I created a sports related activity for students. What makes it special is that I got the information from the children’s book The Economics of the Super Bowl.

What makes it even cooler is that students can read the book for free on Epic. However, in the text the numbers are already in order, so you may want to wait and use the book as a self checking strategy.
Distance Learning
Since many of us are unsure of how frequently we will actually be with our students, there is a digital version of each lesson. If an interactive element was needed, those are included in the digital version.

Each of the lessons above are a portion of my 4th Grade Place Value Unit. If you already own the unit or the bundle, you can access all of the new lessons and digital updates by downloading the file again.
Anchor Charts
After finishing the unit, I hang up my Math Anchor Charts that are a bit smaller than my anchor charts. No matter how hard I try, trace, measure, outline…you name it….I cannot make a nice looking anchor chart, so I hang these up for my students to reference throughout the year. I also have a third grade version of the anchor charts.



