
This post includes some of my favorite lessons for teaching students to compare fractions with strategies such as: common numerator, common denominator, benchmark numbers, the missing piece, and equivalent fractions. The goal of the lessons is to help students develop concepts of relative fraction sizes. These conceptual lessons should be taught BEFORE students learn tricks for comparing fractions. You can find all of the lessons below here.
When teaching students to compare fractions, it’s important to help students understand when talking about the size of a fraction you are not referring to the size of the digits in a fraction. It’s also important that students understand that when comparing fractions, they must refer to the same size whole.
I like to introduce comparing fractions with a whole group lesson that introduces four ways to compare fractions. Since equivalent fractions are a bit trickier, I save that for the next lesson.

Students learn to compare fractions with like numerators and like denominators in third grade, so that’s often the easiest place to begin. Students should use models to develop and understanding of WHY the rules work.
- When fractions have common denominators the fraction with the larger numerator has the greatest value.
- When fractions have common numerators, the fraction with the smallest denominator has the greatest value.

If students are working digitally, their books would like the image below. When introducing the missing piece, students should compare fractions that are one unit away from a whole. The fraction “missing” a larger piece is the smaller fraction.

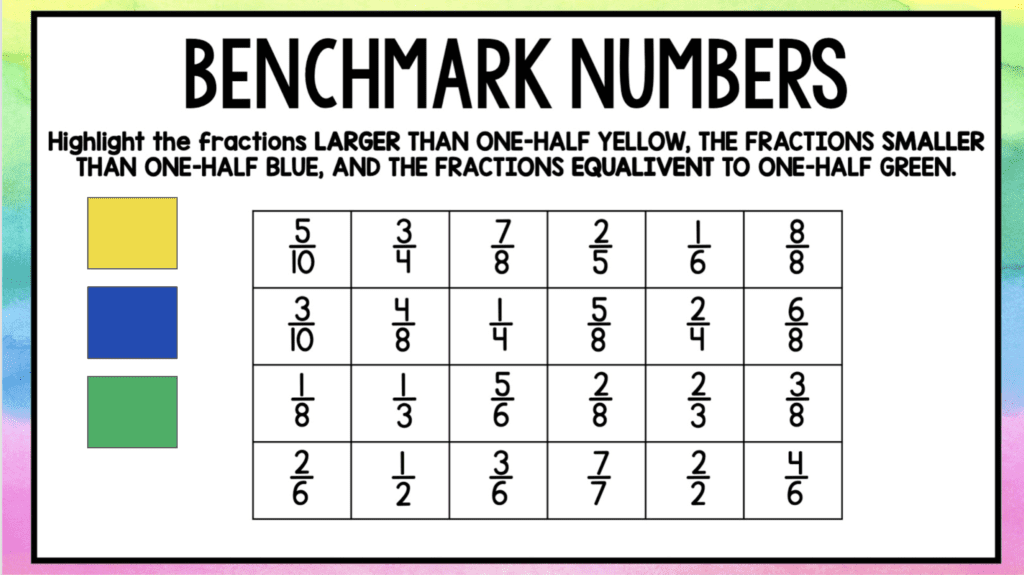
Students should also think about the size of fractions in relation to benchmark numbers. One way to do this is to have students highlight the fractions equivalent to one-half green, fractions greater than one-half yellow, and fractions smaller than one-half blue.
Comparing Fractions Practice
In the following lesson, I like to give students additional practice comparing fractions. This is also when I teach students how to create an equivalent fraction to compare fractions. Th lesson allows me to see who needs small group support. You can either print these task cards of use the digital form for the extra practice. This is great reinforcement because it allows you to see how students are using comparing fraction strategies. You can download the task cards for free here.

Problem Solving
Once students have a general understanding of how to compare fractions, it’s important to incorporate problem solving activities. This allows students to apply what they’ve learned in authentic situations.

These lessons can also be completed digitally. They contain the same content but are presented in a different format.

Of course, students favorite lesson is always the Skittle Fraction lesson! In this activity, students find the fractional part of each color fraction in a bag of Skittles. Then, they find two partners (each with a different denominator) to compare the fractional part of each color with.

These lessons help solidify understanding of fraction size and allow students to continue developing their fraction sense. You can find each of the lessons above here.
If you’re looking for more blog posts on teaching fractions, don’t miss this! It’s the home-base for all of my fraction posts.


