
High quality math interventions are not easy to find. I can access plenty of digital programs-some that I like, some that I don’t. But, students need more than practice on the computer. They need hands-on, guided lessons that provide authentic learning experiences.
Since I’m responsible for my students’ math interventions, I ended up creating my own math interventions (you can find them here). I use these remediation lessons along with district approved computer programs. As always, time is my biggest struggle. Thankfully, a lack of resources is no longer adding to the challenge.
This post shares lessons I use for division interventions. If you’d like to read more about other math topics, you can find those links below.
Division Interventions -General Concept
The division intervention lessons begin with the concept of basic division. Students can often recite a definition, “division in repeated subtraction” or “division is creating equal groups” but they have no idea what those statements mean. When needed, I bring students back to the very beginning.
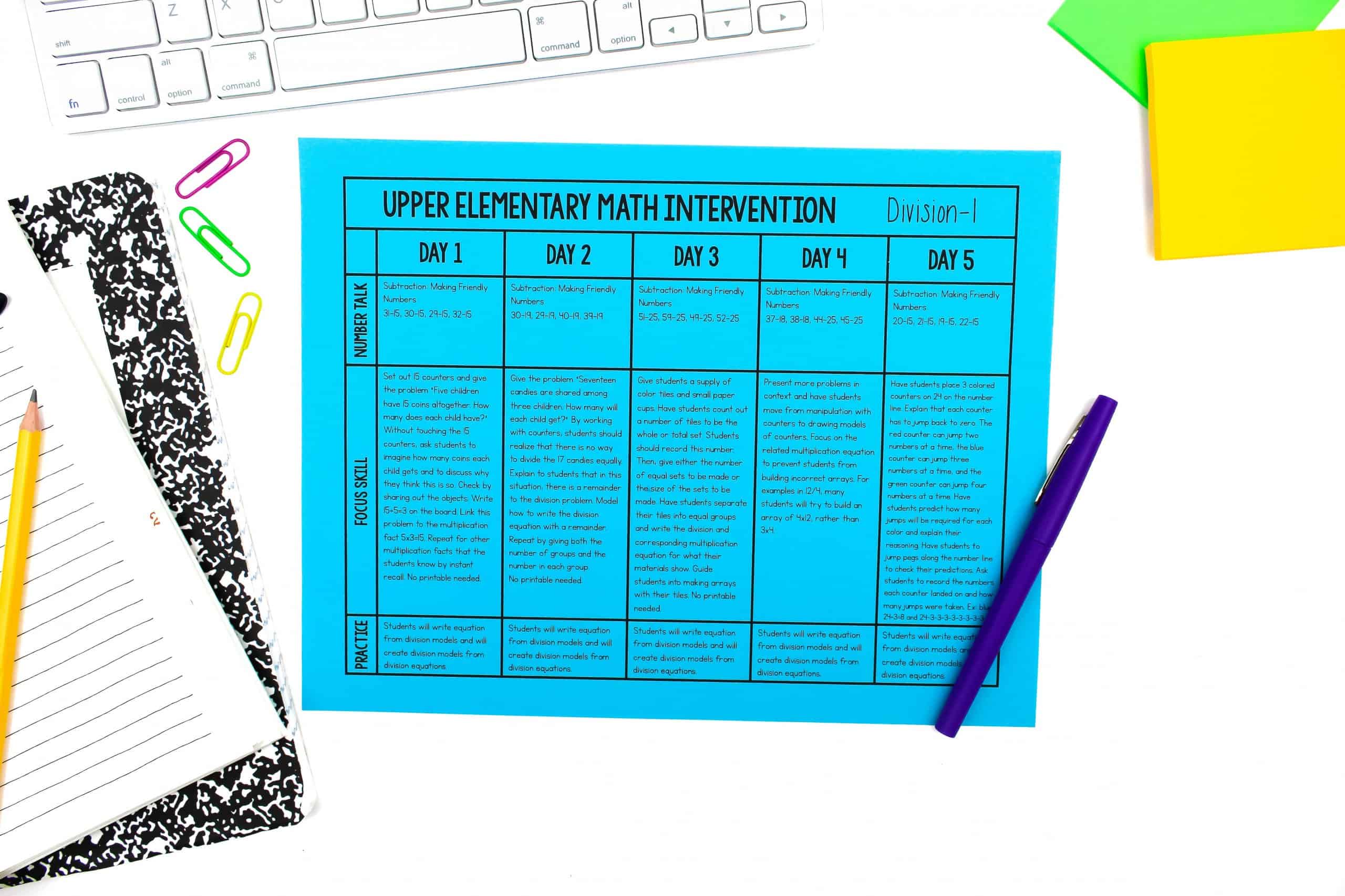
Hands-On Lessons
This lesson is a great way to get students thinking about division. Set out 15 counters and give the problem “Five children have 15 coins altogether. How many does each child have?” Without touching the 15 counters, ask students to imagine how many coins each child gets and to discuss why they think this is so.
Have students check their prediction by sharing out the objects. Write 15÷5=3 on the board. Link this problem to the multiplication fact 5×3=15. Repeat for other division problems.
This activity introduces remainders. Give the problem, “Seventeen candies are shared among three children. How many will each child get?” By working with counters, students should realize that there is no way to divide the 17 candies equally. Explain to students that in this situation, there is a remainder to the division problem. Model how to write the division equation with a remainder. Continue with other numbers and by giving both the number of groups and the number in each group.
Visual Representations
Eventually, you should present problems in context and have students move from manipulatives to drawing models. During this time, help students focus on the related multiplication equation to prevent students from building incorrect arrays. For example in 12÷4, many students will try to build an array of 4×12, rather than 3×4.

During division interventions, students benefit from seeing division on a number line. One way to incorporate number lines is to have students place 3 colored counters on 24 on the number line. Explain that each counter has to jump back to zero. The red counter can jump two numbers at a time, the blue counter can jump three numbers at a time, and the green counter can jump four numbers at a time. Have students predict how many jumps will be required for each color and explain their reasoning. Have students jump pegs along the number line to check their predictions. This is a great way to connect division with repeated subtraction.

Division Interventions-Multiples of 10
If you’re teaching 4th or 5th grade, you may need to provide interventions with multi digit division. One lesson I enjoy is to give students a number such as 3,800. Have students make this number with dotty array pieces. Explain that you want to equally share the dots into ten equal groups. Have students predict how many dots will be in each group. Show students how the result of dividing 3,800 by 10 can be shown on a place value chart. The effect of dividing by 10 is to shift the digits of the dividend one place to the right. This activity can be repeated until students accurately divide by 10.

When dividing by multiples of ten, money can be a useful tool. Place 37 pennies on the table and ask, “How many dimes can I exchange these pennies for?” Model how to solve by placing groups of 10 pennies on different index cards. (The index cards represent a group). Count out the remaining 7 pennies and leave them on the desk. Show how to write the problem as a division equation. Continue to give students additional penny problems where they count out groups of ten and complete the sentence stems.

This can extended using dimes and dollars. Place 26 dimes on the table and ask, “How many dollars can I exchange these dime=es for?” Model how to solve by placing groups of 10 dimes on index cards. (The index cards represent a group.) Count out the remaining 6 dimes and leave them on the desk. Show how to write the problem as a division equation. Give students additional dime problems. Have students count out groups of ten and complete the sentence stems.

To further prepare students, have students build a 3-digit number with base-ten blocks (or dot paper) and have students divide that number by ten. Students will quickly see that there is a large remainder. Discuss why the remainder to these problems can be large. Repeat until students begin to see a pattern. You can also build a 4-digit number and divide that number by 100.

Division Interventions-Multi-Digit Division
These lessons allow students to understand multi-digit division. Have students build a build 2-digit number with base-ten blocks. Then, have students place the blocks into groups of a given number. After ample experience with the base-ten blocks, have students complete the recording sheet which uses visual representations.

When students are ready to move forward, model how to solve a division problem using an area model on grid paper. The second page of the lesson includes the same style of grid paper, but the lines in the center are barely visible. This is preparing students for solving division problems without using any grid paper through area models.


Once students have experience solving 2-digit division problems, they are ready to venture into solving 3-digit problems. This will allow students to apply what they’ve learned about dividing by 100 in previous lessons. First have students divide 3-digit numbers using base-ten blocks. Students will have to regroup remaining hundreds and tens as they divide. After ample experience with base-ten blocks, have students complete the recording sheet with visual representations.

Once again, the second page includes the same style of grid paper, but the lines in the center are barely visible. This is preparing students for solving division problems without using any grid paper through area models. I like to encourage students to shade in groups of ten one color and ones a different color.


Division Interventions-Partial Quotient
I absolutely believe in teaching conceptually, but there are times when I do have to focus on the procedure first. Some students do not naturally connect area models to partial quotient, and these lessons support those students. I have included this as a freebie here!



The math intervention lessons can be found here!


